题目内容
 如图,已知△ABC和△DEF都是等边三角形,O为BC、EF的中点,请找出与△BOE相似的三角形并给出证明.
如图,已知△ABC和△DEF都是等边三角形,O为BC、EF的中点,请找出与△BOE相似的三角形并给出证明.考点:相似三角形的判定,等边三角形的性质
专题:
分析:由已知可以推出OB:OA=OE:OD,推出△ODA∽△OEB,
解答:解:∵△ABC与△DEF均为等边三角形,O为BC、EF的中点,
∴AO⊥BC,DO⊥EF,∠EDO=30°,∠BAO=30°,
∴OD:OE=OA:OB=
:1,
∵∠DOE+∠EOA=∠BOA+∠EOA 即∠DOA=∠EOB,
∴△DOA∽△EOB.
∴AO⊥BC,DO⊥EF,∠EDO=30°,∠BAO=30°,
∴OD:OE=OA:OB=
| 3 |
∵∠DOE+∠EOA=∠BOA+∠EOA 即∠DOA=∠EOB,
∴△DOA∽△EOB.
点评:本题主要考查了相似三角形的判定、等边三角形的性质,本题的关键在于找到需要证相似的三角形,找到对应边的比即可.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 同心圆⊙O中,小⊙O和⊙O的半径分别是2
同心圆⊙O中,小⊙O和⊙O的半径分别是2| 10 |
| 5 |
A、15
| ||
B、4
| ||
C、5
| ||
D、8
|
无论m为何实数,直线y=(m-1)x+m必过一定点,此点的坐标为( )
| A、(-1,1) |
| B、(1,1) |
| C、(0,1) |
| D、(1,-1) |
 如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长.
如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长. 如图,?ABCD的对角线的交点为点O,点E为CD中点,若S?ABCD=24cm2,求S△AOE的值.
如图,?ABCD的对角线的交点为点O,点E为CD中点,若S?ABCD=24cm2,求S△AOE的值.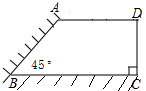 校园要建苗圃,其形状如直角梯形,有两边借用夹角为45°的两面墙,如图,另外两边是总长为30m的铁栅栏.
校园要建苗圃,其形状如直角梯形,有两边借用夹角为45°的两面墙,如图,另外两边是总长为30m的铁栅栏.