题目内容
 如图,?ABCD的对角线的交点为点O,点E为CD中点,若S?ABCD=24cm2,求S△AOE的值.
如图,?ABCD的对角线的交点为点O,点E为CD中点,若S?ABCD=24cm2,求S△AOE的值.考点:平行四边形的性质
专题:
分析:根据平行四边形对角线互相平分可得AO=CO,再根据三角形的中线把三角形分成两个面积相等的三角形分别求出△ACE和△AOE即可.
解答:解:∵?ABCD的对角线的交点为点O,
∴AO=CO,
∵S?ABCD=24cm2,
∴S△ACD=
S?ABCD=
×24=12cm2,
∵点E为CD中点,
∴S△ACE=
S△ACD=
×12=6cm2,
∵AO=CO,
∴S△AOE=
S△ACE=
×6=3cm2.
∴AO=CO,
∵S?ABCD=24cm2,
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∵点E为CD中点,
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AO=CO,
∴S△AOE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了平行四边形的性质,三角形的面积,熟练掌握三角形的中线把三角形分成两个面积相等的三角形是解题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 如图,已知图形(矩形+正三角形)的周长为6-
如图,已知图形(矩形+正三角形)的周长为6-| 3 |
6-
| ||
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知△ABC和△DEF都是等边三角形,O为BC、EF的中点,请找出与△BOE相似的三角形并给出证明.
如图,已知△ABC和△DEF都是等边三角形,O为BC、EF的中点,请找出与△BOE相似的三角形并给出证明. 如图,四边形ABCD中,AD∥BC,AC与BD交于点P,点P是BD的黄金分割点(BP大于PD),已知AD=1,求BC的长.
如图,四边形ABCD中,AD∥BC,AC与BD交于点P,点P是BD的黄金分割点(BP大于PD),已知AD=1,求BC的长.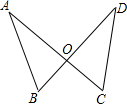 如图,已知AC=BD,AB=DC,求证:△AOB≌△DOC.
如图,已知AC=BD,AB=DC,求证:△AOB≌△DOC.