题目内容
17.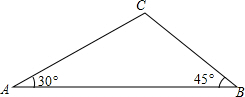 如图,在△ABC中,∠A=30°,∠B=45°,AB=12+12$\sqrt{3}$,求△ABC的面积.
如图,在△ABC中,∠A=30°,∠B=45°,AB=12+12$\sqrt{3}$,求△ABC的面积.
分析 作CH⊥AB于H,如图,设CH=x,在Rt△ACH中利用含30度的直角三角形三边的关系得AH=$\sqrt{3}$CH=$\sqrt{3}$x,在Rt△CBH中,根据等腰直角三角形的性质得BH=CH=x,则AB=BH+AH=x+$\sqrt{3}$x,原式可得到方程$\sqrt{3}$x+x=12+12$\sqrt{3}$,解方程得到x=12,然后根据三角形面积公式求解.
解答 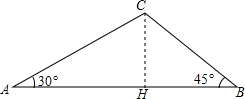 解:作CH⊥AB于H,如图,设CH=x,
解:作CH⊥AB于H,如图,设CH=x,
在Rt△ACH中,∵∠A=30°,
∴AH=$\sqrt{3}$CH=$\sqrt{3}$x,
在Rt△CBH中,
∵∠B=45°,
∴BH=CH=x,
∴AB=BH+AH=x+$\sqrt{3}$x,
∴$\sqrt{3}$x+x=12+12$\sqrt{3}$,
∴x=12,
∴△ABC的面积=$\frac{1}{2}$CH•AB=$\frac{1}{2}$×12×(12+12$\sqrt{3}$)=72$\sqrt{3}$+72.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.充分利用特殊角的三角函数值解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 30°或50° |
8.圆内最大的弦长为10cm,则圆的半径( )
| A. | 小于5cm | B. | 大于5cm | C. | 等于5cm | D. | 不能确定 |
5. 如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )
如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )
 如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )
如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )| A. | AB>2CD | B. | AB=2CD | C. | AB<2CD | D. | 以上都不正确 |
6.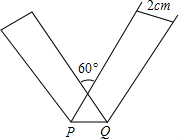 将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
 将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )| A. | $\frac{2}{3}$$\sqrt{3}$cm | B. | $\frac{4}{3}$$\sqrt{3}$cm | C. | $\sqrt{5}$cm | D. | 2cm |
 如图,∠MCF=∠FCD,∠MCE=∠ECB,EF=10cm,则CE2+CF2=100cm2.
如图,∠MCF=∠FCD,∠MCE=∠ECB,EF=10cm,则CE2+CF2=100cm2.