题目内容
2.已知△ABC的三条边长分别为3cm,4cm,5cm,△ABC∽△A′B′C′,那么△A′B′C′的形状是直角三角形.分析 先根据勾股定理的逆定理判断出△ABC的形状,再由相似三角形的性质即可得出结论.
解答 解:∵△ABC的三条边长分别为3cm,4cm,5cm,32+42=52,
∴△ABC是直角三角形.
∵△ABC∽△A′B′C′,
∴△A′B′C′是直角三角形.
故答案为:直角三角形.
点评 本题考查的是相似三角形的性质,熟知相似三角形的对应角相等是解答此题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17.三元一次方程组$\left\{\begin{array}{l}{3x-2y=5}\\{x+y+z=2}\\{z=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\\{z=2}\end{array}\right.$ |
7. 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 30°或50° |
14.△ABC的三边长分别为$\sqrt{2}$,$\sqrt{10}$和2,△A′B′C′的两边长分别为1和$\sqrt{5}$.如果△ABC∽△A′B′C′,则
△A′B′C′第三边的长为( )
△A′B′C′第三边的长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
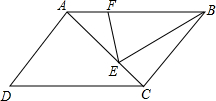 平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,求平行四边形ABCD的面积.
平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,求平行四边形ABCD的面积.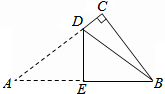 如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm.
如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm. 如图,直线AB⊥l1,l1∥l2,∠1=75°,则∠2的大小为165°.
如图,直线AB⊥l1,l1∥l2,∠1=75°,则∠2的大小为165°. 如图,∠MCF=∠FCD,∠MCE=∠ECB,EF=10cm,则CE2+CF2=100cm2.
如图,∠MCF=∠FCD,∠MCE=∠ECB,EF=10cm,则CE2+CF2=100cm2.