题目内容
2.已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE=1:$\sqrt{7}$:3,求∠AED的度数;
(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=$\frac{\sqrt{5}}{3}$,求CN的长.
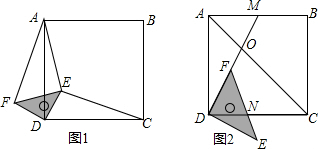
分析 (1)由正方形额等腰直角三角形的性质判断出△ADF≌△CDE即可;
(2)设DE=k,表示出AE,CE,EF,判断出△AEF为直角三角形,即可求出∠AED;
(3)由AB∥CD,得出$\frac{OM}{OD}=\frac{OA}{OC}=\frac{AM}{DC}$=$\frac{1}{2}$,求出DM,DO,再判断出△DFN∽△DCO,得到$\frac{DF}{DC}=\frac{DN}{DO}$,求出DN即可.
解答 (1)CE=AF;
证明:在正方形ABCD,等腰直角三角形CEF中,FD=DE,CD=CA,∠ADC=∠EDF=90°
∴∠ADF=∠CDE,
∴△ADF≌△CDE,
∴CE=AF,
(2)设DE=k,
∵DE:AE:CE=1:$\sqrt{7}$:3
∴AE=$\sqrt{7}$k,CE=AF=3k,
∴EF=$\sqrt{2}$k,
∵AE2+EF2=7k2+2k2=9k2,AF2=9k2,
即AE2+EF2=AF2
∴△AEF为直角三角形,
∴∠BEF=90°
∴∠AED=∠AEF+DEF=90°+45°=135°;
(3)∵M是AB中点,
∴MA=$\frac{1}{2}$AB=$\frac{1}{2}$AD,
∵AB∥CD,
∴$\frac{OM}{OD}=\frac{OA}{OC}=\frac{AM}{DC}$=$\frac{1}{2}$,
在Rt△DAM中,DM=$\sqrt{A{D}^{2}+A{M}^{2}}$=$\sqrt{16+4}$=2$\sqrt{5}$,
∴DO=$\frac{4\sqrt{5}}{3}$,
∵OF=$\frac{\sqrt{5}}{3}$,
∴DF=$\sqrt{5}$,
∵∠DFN=∠DCO=45°,∠FDN=∠CDO,
∴△DFN∽△DCO,
∴$\frac{DF}{DC}=\frac{DN}{DO}$,
∴$\frac{\sqrt{5}}{4}=\frac{DN}{\frac{4\sqrt{5}}{3}}$,
∴DN=$\frac{5}{3}$,
∴CN=CD-DN=4-$\frac{5}{3}$=$\frac{7}{3}$.
点评 此题是几何变换综合题,主要考查了正方形,等腰直角三角形的性质,全等三角形的性质和判定,相似三角形的性质和判定,勾股定理及其勾股定理的逆定理,判断△AEF为直角三角形是解本题的关键,也是难点.

| A. | m<3 | B. | m≤3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y3<y1 |
| 月用水量(m3) | 4 | 6 | 7 | 12 | 14 | 15 |
| 户数 | 2 | 4 | 6 | 2 | 2 | 4 |
(2)计算这20户家庭的平均月用水量;
(3)根据上述数据,估计该小区300户家庭的月总用水量.
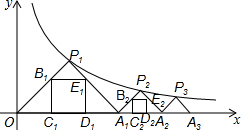 如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1,△P2A1A2的内接正方形的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则l1+l2+l3+…+ln=$\frac{8}{3}$$\sqrt{n}$(用含n的式子表示).
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1,△P2A1A2的内接正方形的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则l1+l2+l3+…+ln=$\frac{8}{3}$$\sqrt{n}$(用含n的式子表示).
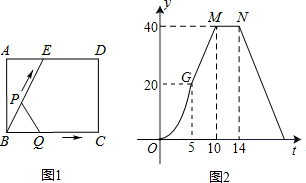 如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①AD=BE=5;②当0<t≤5时,y=$\frac{4}{5}$t2;③cos∠ABE=$\frac{3}{5}$;④当t=$\frac{29}{2}$秒时,△ABE∽△QBP;⑤当△BPQ的面积为4cm2时,时间t的值是$\sqrt{10}$或$\frac{51}{5}$; 其中正确的结论是②④.
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①AD=BE=5;②当0<t≤5时,y=$\frac{4}{5}$t2;③cos∠ABE=$\frac{3}{5}$;④当t=$\frac{29}{2}$秒时,△ABE∽△QBP;⑤当△BPQ的面积为4cm2时,时间t的值是$\sqrt{10}$或$\frac{51}{5}$; 其中正确的结论是②④.