题目内容
3.若变量y与变量x的函数关系是y=-(x-m)2-m2+5,在-1≤x≤3范围内的最大值为4,则常数m的值是3.分析 分m<-1,-1≤m≤3和m>3三种情况,根据二次函数的增减性列方程求解即可.
解答 解:若m<-1,则x=-1时,二次函数有最大值,此时=-(-1-m)2-m2+5=4,
解得m=0,m=1(不符合题意),
若-1≤x≤3,则x=m时,二次函数有最大值-m2+5=4,
解得m=±3,m=-3(舍去),
∴m=3,
若m>3,则x=3时,二次函数有最大值,此时=-(3-m)2-m2+5=4,
方程无实数根,
综上所述,a的值等于3.
故答案为3.
点评 本题考查了二次函数的最值问题,主要利用了二次函数的增减性,难点在于分情况讨论.

练习册系列答案
相关题目
13.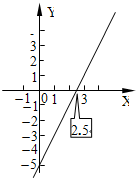 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
( )
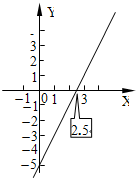 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是( )
| A. | x>2.5 | B. | x<2.5 | C. | x>-5 | D. | x<-5 |
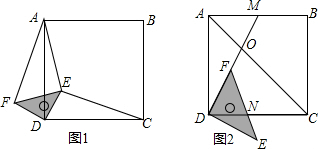
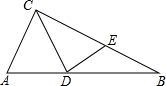 如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.
如图,在Rt△ABC中,∠C=90°,AC=3,将△ACD沿CD翻折,使点A落在BC的中点E处,则点D到BC的距离是2.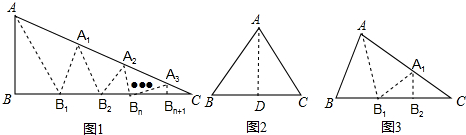
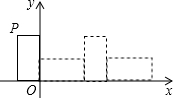 如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).
如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).