题目内容
1. 如图,直线AB与CD相交于点O,射线OE⊥直线AB,若∠COE=49°23′,则∠BOD=40°37′.
如图,直线AB与CD相交于点O,射线OE⊥直线AB,若∠COE=49°23′,则∠BOD=40°37′.
分析 根据垂直的定义可得∠BOE=90°,∠COE+∠BOE+∠BOD=180°,列出算式计算即可求解.
解答 解:∵射线OE⊥直线AB,∠COE=49°23′,
∴∠BOD=180°-∠BOE-∠COE
=180°-90°-49°23′
=40°37′
故答案为:40°37′.
点评 本题考查平角和垂线的概念,关键是从图中看到哪些角的和是90度,哪些角的和是180度.

练习册系列答案
相关题目
13.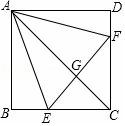 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
.其中正确结论有( )
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC.其中正确结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.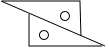 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
 如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )
如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 以上都不对 |
11. 如图,点D在AC的垂直平分线上,AB∥CD.若∠BAC=25°,则∠D的度数是( )
如图,点D在AC的垂直平分线上,AB∥CD.若∠BAC=25°,则∠D的度数是( )
 如图,点D在AC的垂直平分线上,AB∥CD.若∠BAC=25°,则∠D的度数是( )
如图,点D在AC的垂直平分线上,AB∥CD.若∠BAC=25°,则∠D的度数是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
 如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是正方形.
如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是正方形.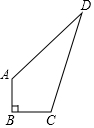 在四边形ABCD中,AB=3,BC=4,CD=13,DA=12,且∠B=90°.求四边形ABCD 的面积.
在四边形ABCD中,AB=3,BC=4,CD=13,DA=12,且∠B=90°.求四边形ABCD 的面积.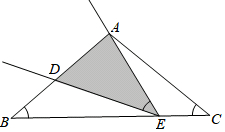 如图,在等腰△ABC中,AB=AC=8cm,BC=10cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.
如图,在等腰△ABC中,AB=AC=8cm,BC=10cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.