题目内容
17.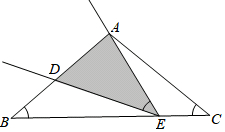 如图,在等腰△ABC中,AB=AC=8cm,BC=10cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.
如图,在等腰△ABC中,AB=AC=8cm,BC=10cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.(1)求证:△BDE∽△CEA;
(2)设BE=x,AD=y,请写y与x之间的函数关系;
(3)E点在运动的过程中,△ADE能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由.
分析 (1)根据∠BDE=∠CEA,∠B=∠C证得结论;
(2)利用(1)中相似三角形的对应边成比例列出比例式$\frac{BD}{EC}$,则把相关线段的长度代入即可列出y与x的关系式.注意自变量x的取值范围要注明;
(3)根据三角形外角性质和三角形的边角关系知AE≠AD.所以当△ADE是等腰三角形时,分两种情况:①当AE=DE时,△BDE≌△CEA;②当DA=DE时,△BAE∽△BCA.所以根据全等三角形和相似三角形的性质来求线段BE的长度.
解答 (1)证明:∵∠BDE=180°-∠DEB-∠B,∠CEA=180°-∠DEB-∠AED,
又∠B=∠AED,
∴∠BDE=∠CEA,
∵AB=AC,
∴∠B=∠C,
∴△BDE∽△CEA;
(2)解:∵△BDE∽△CEA,
∴$\frac{BD}{EC}$=$\frac{BE}{AC}$, 即 $\frac{8-y}{10-x}$=$\frac{x}{8}$,
即 $\frac{8-y}{10-x}$=$\frac{x}{8}$,
∴y=$\frac{1}{8}$x2-$\frac{5}{4}$x+8(0<x<8),
(3)解:∵∠ADE是△BDE的外角,
∴∠ADE>∠B,
∵∠B=∠AED,
∴∠ADE>∠AED,
∴AE≠AD.
①当AE=DE时,
得△BDE≌△CEA,
∴BE=AC=8cm;
②当DA=DE时,∠BAE=∠AED=∠C,
又∵∠B=∠B,
∴△BAE∽△BCA,
∴$\frac{BA}{BC}$=$\frac{BE}{BA}$,
即:$\frac{8}{10}$=$\frac{BE}{8}$,
∴BE=$\frac{32}{5}$cm,
∴△ADE为等腰三角形时,BE=6cm或 $\frac{32}{5}$cm
点评 本题考查了相似三角形的判定与性质、三角形外角的性质,二次函数的最值等知识点.解答(3)题时,要分类讨论,以防漏解.

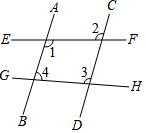 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )| A. | 如果EF∥GH,那么∠4+∠3=180° | B. | 如果AB∥CD,那么∠1+∠4=180° | ||
| C. | 如果AB∥CD,那么∠1=∠2 | D. | 如果AB∥CD,那么∠2=∠3 |
| A. | $\sqrt{2.5}$ | B. | $\root{3}{-64}$ | C. | 1.5151151115 | D. | $\frac{7π}{2π}$ |
| A. | 两条射线所组成的图形叫角 | |
| B. | 角的大小与所画的角的边的长短无关 | |
| C. | 角的两边是两条线段 | |
| D. | 角的两边是两条直线 |
 如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )
如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )| A. | 120° | B. | 130° | C. | 150° | D. | 90° |
 如图,三条直线a,b,c两两相交,则到三条直线距离相等的点有4个.
如图,三条直线a,b,c两两相交,则到三条直线距离相等的点有4个. 如图,直线AB与CD相交于点O,射线OE⊥直线AB,若∠COE=49°23′,则∠BOD=40°37′.
如图,直线AB与CD相交于点O,射线OE⊥直线AB,若∠COE=49°23′,则∠BOD=40°37′. 如图,直线a∥b,∠1=54°,则∠2=54°.
如图,直线a∥b,∠1=54°,则∠2=54°.