题目内容
13.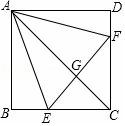 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①∠DAF=15°,②AC垂直平分EF,③BE+DF=EF,④AF=$\sqrt{2}$EC.其中正确结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据全等三角形的性质以及等边三角形、正方形的性质,即可得到∠DAF=15°;根据CE=CF,AE=AF,即可得出AC垂直平分EF;设EG=GF=CG=1,根据BE+DF=$\sqrt{6}$-$\sqrt{2}$,EF=2,即可得到BE+DF≠EF;根据等腰Rt△CEF中,EF=$\sqrt{2}$CE,且△AEF是等边三角形,可得AF=$\sqrt{2}$EC.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AE=AF}\\{AB=AD}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF,BE=DF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,故①正确.
∵BC=CD,BE=DF,
∴BC-BE=CD-DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF,故②正确.
设EG=GF=CG=1,则CE=$\sqrt{2}$,AG=$\sqrt{3}$,
∴AC=$\sqrt{3}$+1,
∴Rt△ABC中,BC=$\frac{AC}{\sqrt{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∴BE=BC-CE=$\frac{\sqrt{6}-\sqrt{2}}{2}$,
∴BE+DF=$\sqrt{6}$-$\sqrt{2}$,
又∵EF=2,
∴BE+DF≠EF,故③错误;
∵等腰Rt△CEF中,EF=$\sqrt{2}$CE,且△AEF是等边三角形,
∴AF=$\sqrt{2}$EC,故④正确;
故选:C.
点评 本题考查了全等三角形的判断和性质,等边三角形和正方形的性质,线段垂直平分线的性质和判定,证得Rt△ABE≌Rt△ADF是解题的关键.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 4cm | B. | 5cm | C. | 小于2cm | D. | 不大于2cm |
| A. | $\sqrt{2.5}$ | B. | $\root{3}{-64}$ | C. | 1.5151151115 | D. | $\frac{7π}{2π}$ |
| A. | $\sqrt{-5}$=-$\sqrt{5}$ | B. | $-\sqrt{3.6}$=-0.6 | C. | $\sqrt{(-6)^{2}}$=6 | D. | $\sqrt{36}$=±6 |
 如图,三条直线a,b,c两两相交,则到三条直线距离相等的点有4个.
如图,三条直线a,b,c两两相交,则到三条直线距离相等的点有4个. 如图,直线AB与CD相交于点O,射线OE⊥直线AB,若∠COE=49°23′,则∠BOD=40°37′.
如图,直线AB与CD相交于点O,射线OE⊥直线AB,若∠COE=49°23′,则∠BOD=40°37′.