题目内容
18. 如图,在⊙O中,直径CD⊥弦AB于E,且E是OD的中点,又AB=6cm,则⊙O的半径为( )
如图,在⊙O中,直径CD⊥弦AB于E,且E是OD的中点,又AB=6cm,则⊙O的半径为( )| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 4 |
分析 连接AO,先根据垂径定理求出AE的长,再由E是OD的中点得出OE=$\frac{1}{2}$OD=$\frac{1}{2}$OA,设OE=x,则OA=2x,在Rt△AOE中根据勾股定理求出x的值,进而可得出结论.
解答 解: 连接AO,在⊙O中,
连接AO,在⊙O中,
∵直径CD⊥弦AB于E,AB=6cm,
∴AE=3cm.
∵E是OD的中点,
∴OE=$\frac{1}{2}$OD=$\frac{1}{2}$OA,
设OE=xcm,则OA=2xcm,
在Rt△AOE中,
∵OE2+AE2=OA2,
∴x2+9=4x2,
∴x=$\sqrt{3}$,
∴OA=2$\sqrt{3}$cm,
即⊙O的半径为2$\sqrt{3}$cm.
故选:B.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3、0)点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,在运动的过程中,当△ABC是以AB为底的等腰三角形时,此时点C的坐标为(0,$\frac{11}{8}$).
如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3、0)点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,在运动的过程中,当△ABC是以AB为底的等腰三角形时,此时点C的坐标为(0,$\frac{11}{8}$).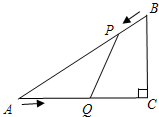 已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?
已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),当t为何值时,以A、P、Q为顶点的三角形与△ABC相似? 我们知道,已知圆心和半径,可以作一个圆.不难理解,经过一个已知点A作圆,能作出无数个.回答下列问题:
我们知道,已知圆心和半径,可以作一个圆.不难理解,经过一个已知点A作圆,能作出无数个.回答下列问题: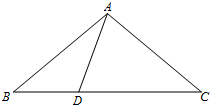 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.