题目内容
8．已知线段AB=10cm，点P是线段AB的黄金分割点，且AP＞PB，则AP≈6.18cm．分析 根据黄金分割的定义求解．
解答 解：∵点P是线段AB的黄金分割点，且AP＞PB，
∴AP=$\frac{\sqrt{5}-1}{2}$AB≈6.18（cm）．
故答案为6.18．
点评 本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB，并且线段AB的黄金分割点有两个．
练习册系列答案
相关题目
19．顶点为（-5，0）形状与函数y=-$\frac{1}{3}$x2的图象相同且开口方向相反的抛物线是（ ）
| A． | y=-$\frac{1}{3}$（x-5）2 | B． | y=-$\frac{1}{3}$x2-5 | C． | y=-$\frac{1}{3}$（x+5）2 | D． | y=$\frac{1}{3}$（x+5）2 |
16．如图，直角三角形纸片ABC中AB=3，AC=4，D为斜边BC中点，第1次将纸片折叠，使点A与点D重合，折痕与AD交于点P1；设P1D的中点为D1，第2次将纸片折叠，使点A与点D1重合，折痕与AD交于P2；设P2D1的中点为D2，第3次将纸片折叠，使点A与点D2重合，折痕与AD交于点P3；设Pn-1Dn-2的中点为Dn-1，第n次将纸片折叠，使点A与点Dn-1重合，折痕与AD交于点Pn（n＞2），则AP6的长为（ ）
| A． | $\frac{{3}^{5}}{5×{2}^{9}}$ | B． | $\frac{5×{3}^{5}}{{2}^{12}}$ | C． | $\frac{5×{3}^{6}}{{2}^{14}}$ | D． | $\frac{{3}^{7}}{5×{2}^{11}}$ |
如图，一边靠校园围墙，其他三边用总长为80米的铁栏杆围成一个矩形花圃，设矩形ABCD的边AB为x米，面积为S平方米，要使矩形ABCD面积最大，则x的长为（ ）
如图，AB=AC，若使△ABE≌△ACF，则还需要添加的条件是∠B=∠C．（只要写出一个答案）．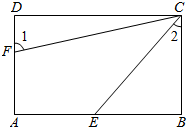
如图，已知四边形ABCD是平行四边形，并且∠A=∠D．
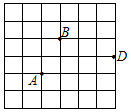如图，在6×6的正方形网格中，每个小正方形边长都是1，每个小正方形的顶点叫做格点．A、B两格点位置如图所示．