题目内容
3.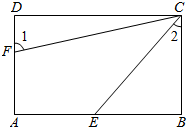 如图,已知四边形ABCD是平行四边形,并且∠A=∠D.
如图,已知四边形ABCD是平行四边形,并且∠A=∠D.(1)求证:四边形ABCD为矩形;
(2)点E是AB边的中点,F为AD边上一点,∠1=2∠2,若CE=4,CF=5,求DF的长.
分析 (1)根据“有一内角为直角的平行四边形是矩形”进行证明;
(2)延长DA,CE交于点G,证明△AGE≌△BCE,得出AG=BC,再证明CF=FG即可,设DF=x,根据勾股定理得出:CD2=CF2-DF2=CG2-DG2,列出方程52-x2=82-(5+x)2,解方程求出x,得DF的长度.
解答 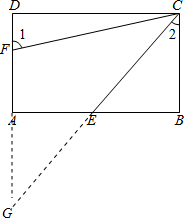 (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A+∠D=180°,
又∠A=∠D,
∴∠A=∠D=90°,
∴平行四边形ABCD为矩形;
(2)解:延长DA,CE交于点G,
∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,AD∥BC,
∴∠GAE=90°,∠G=∠ECB,
∵E是AB边的中点,
∴AE=BE,
在△AGE和△BCE中,$\left\{\begin{array}{l}{∠G=∠ECB}\\{∠GAE=∠B=90°}\\{AE=BE}\end{array}\right.$,
∴△AGE≌△BCE(AAS),
∴AG=BC,
若CE=4,CF=5,
设DF=x,
根据勾股定理得:CD2=CF2-DF2=CG2-DG2,
即52-x2=82-(5+x)2,
解得:x=$\frac{7}{5}$,即DF=$\frac{7}{5}$.
点评 本题考查了矩形的判定与性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理的运用;本题有一定难度,特别是(2)中,需要通过作辅助线证明三角形全等和运用勾股定理才能得出结果.

练习册系列答案
相关题目
7.如果x2-mx+36是一个完全平方式,则m的值为( )
| A. | 6 | B. | 12 | C. | ±6 | D. | ±12 |
15.将式子(-1)×(-1$\frac{1}{2}$)÷$\frac{2}{3}$中的除法转化为乘法运算,正确的是( )
| A. | (-1)×(-$\frac{3}{2}$)×$\frac{2}{3}$ | B. | (-1)×(-$\frac{3}{2}$)×$\frac{3}{2}$ | C. | (-1)×(-$\frac{2}{3}$)×$\frac{3}{2}$ | D. | (-1)×(-$\frac{2}{3}$)×$\frac{2}{3}$ |
13.下列四组数值中,哪些不是二元一次方程x-3y=1的解( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=10}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-5}\\{y=-2}\end{array}\right.$ |
 如图,要在燃气管道l上修建一个泵站,分别向A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律?
如图,要在燃气管道l上修建一个泵站,分别向A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律?