Question

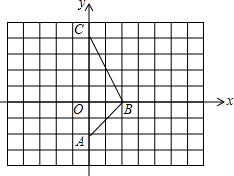在方格纸中，以格点连线为边的三角形叫做格点三角形，如图，已知△ABC是格点三角形，每个小正方形的边长是1．
（1）在如图的直角坐标中，写出△ABC三个顶点的坐标．
A（

 

，

 

）   
B（

 

，

 

）     
C（

 

，

 

）
（2）线段BC的长度为

 

．
（3）在方格纸中画出与△ABC相似的格点三角形△A′B′C′，并使△ABC与△A′B′C′的相似比为2．

Answer 1

考点：作图—相似变换

专题：

分析：（1）根据已知坐标系，得出各点坐标即可；
（2）利用勾股定理得出答案即可；
（3）利用相似三角形的判定与性质，得出符合题意的图形．

解答：解：（1）如图所示：A（0，-2）B：（2，0）C：（0，4）；
故答案为：（0，-2）；（2，0）；（0，4）；

（2）BC=

CO2+BO2

=2

5

；
故答案为：2

5

；

（3）如图所示：△A′B′C′即为所求．

点评：此题主要考查了相似变换以及勾股定理，得出对应线段的长是解题关键．