题目内容
叙述勾股定理的内容,并画出示意图,写出证明过程.
考点:勾股定理的证明
专题:
分析:勾股定理为直角三角形的三边之间的平方关系,结合图形可以利用等积法来证明.
解答:解:勾股定理:直角三角形两直角边的平方和等于斜边的平方.
证明如下:
如图,四个直角三角形(两直角边分别为a、b,斜边长为c)构成一个大的正方形,中间构成一个小的正方形,

则S形方形EFGH=S正方形ABCD-4S△ABF,
即
(a-b)2=
c2-4×
ab,
整理可得a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
证明如下:
如图,四个直角三角形(两直角边分别为a、b,斜边长为c)构成一个大的正方形,中间构成一个小的正方形,

则S形方形EFGH=S正方形ABCD-4S△ABF,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理可得a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
点评:本题主要考查勾股定理的证明,等积法是证明勾股定理的常用方法,即通过两个不同的角度表示出同一个图形的面积,从而得到等量关系.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若多项式2x2+3y的值是1,那么多项式4x2+6y-2的值是( )
| A、0 | B、1 | C、2 | D、3 |
下列各式中,是代数式并且书写各式规范的是( )
A、3
| ||
| B、a+b=b+a | ||
| C、3xy÷5 | ||
D、
|
下列从左到右的变形,是分解因式的是( )
| A、x(a-b)=ax-bx |
| B、x2-1+y2=(x-1)(x+1)+y2 |
| C、ax+bx+c=x(a+b)+c |
| D、x2-1=(x+1)(x-1) |
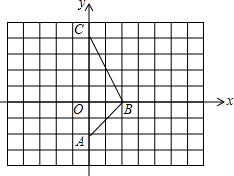 在方格纸中,以格点连线为边的三角形叫做格点三角形,如图,已知△ABC是格点三角形,每个小正方形的边长是1.
在方格纸中,以格点连线为边的三角形叫做格点三角形,如图,已知△ABC是格点三角形,每个小正方形的边长是1.