Question

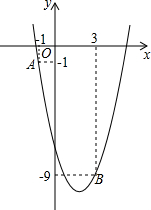 如图，抛物线y=ax²-4x+c经过A（-1，-1）和B（3，-9）．
（1）求该二次函数的表达式；
（2）直接写出当y＞0时，x的取值范围；
（3）若点P（m，m）在该函数图象上，求点P的坐标．

Answer 1

考点：待定系数法求二次函数解析式,二次函数图象上点的坐标特征,二次函数与不等式（组）

专题：

分析：（1）把点的坐标代入二次函数表达式，利用待定系数法求解即可；
（2）令y=0，求出抛物线与x轴的交点，然后根据二次函数的性质两交点之间的x的取值范围就是所求的范围．
（3）把P（m，m）代入y=x²-4x-6，得m=m²-4m-6，解方程即可求得m的值，从而求得P的坐标．

解答：解：（1）根据题意得，

a+4+c=-1 9a-12+c=-9

，
解得

a=1 c=-6

，
所以抛物线的解析式为y=x²-4x-6；

（2）令x²-4x-6=0，
解得x₁=2+

10

，x₂=2-

10

，
根据二次函数的性质可得y＞0时x的取值范围是：x＜2-

10

或x＞2+

10

．

（3）把P（m，m）代入y=x²-4x-6，得m=m²-4m-6，
解得，m₁=-1，m₂=6，
∴P点的坐标为（-1，-1）或（6，6）．

点评：本题考查了待定系数法求二次函数解析式，二次函数图象上点的坐标特征，二次函数的性质，求出函数解析式是解题的关键．