题目内容
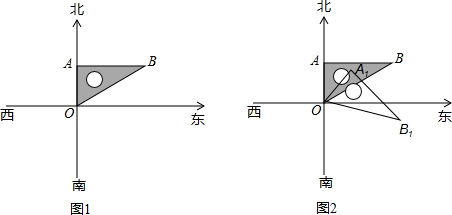
将一个含60°角的直角三角板OAB,(∠OAB=60°)如图1放置,射线OA表示正北方向,
(1)观察图形回答:
①B在O点的 方向.
②O在B点的 方向.
③B在A点的 方向.
④A在B点的 方向.
(2)如图2,将此三角板绕O点顺时针旋转40°角到三角板OA1B1位置,试问B1在O点的什么方向?说明理由.
(3)如图2,图中以O为顶点,OA,OA1,OB,OB1为边构成的角共有多少个?写出它们,并求出这些角的和.
(4)再将三角板OA1B1绕O点顺时针旋转α角到三角板OA2B2位置,若点A2在O点的西南方向,求α的度数并说出B2在O点的什么方向?

(1)观察图形回答:
①B在O点的
②O在B点的
③B在A点的
④A在B点的
(2)如图2,将此三角板绕O点顺时针旋转40°角到三角板OA1B1位置,试问B1在O点的什么方向?说明理由.
(3)如图2,图中以O为顶点,OA,OA1,OB,OB1为边构成的角共有多少个?写出它们,并求出这些角的和.
(4)再将三角板OA1B1绕O点顺时针旋转α角到三角板OA2B2位置,若点A2在O点的西南方向,求α的度数并说出B2在O点的什么方向?
考点:方向角
专题:
分析:(1)直接利用三角形内角度数,再利用方向角得出答案;
(2)根据题意求出∠COB1的度数进而得出答案;
(3)利用旋转角得出∠AOA1+∠AOB+∠AOB1+∠A1OB+∠A1OB1+∠BOB1的和即可;
(4)根据题意得出α=∠A1OA2=90°-40°+90°+45°求出即可.
(2)根据题意求出∠COB1的度数进而得出答案;
(3)利用旋转角得出∠AOA1+∠AOB+∠AOB1+∠A1OB+∠A1OB1+∠BOB1的和即可;
(4)根据题意得出α=∠A1OA2=90°-40°+90°+45°求出即可.
解答:解:(1)①B在O点的北偏东60°方向.
②O在B点的南偏西60°方向.
③B在A点的正东方向.
④A在B点的正西方向;
(2)∵三角板绕O点顺时针旋转40°角,
∴∠AOB1=40°+60°=100°,
∴∠COB1=100°-90°=10°,
∴B1在O点南偏东80°方向;
(3)∠AOA1,∠AOB,∠AOB1,∠A1OB,∠A1OB1,∠BOB1,共6个;
∵三角板绕O点顺时针旋转40°角,
∴∠AOA1=40°,
∴∠AOA1+∠AOB+∠AOB1+∠A1OB+∠A1OB1+∠BOB1=40°+60°+100°+20°+60°+40°=320°;
(4)如图所示:∵点A2在O点的西南方向,
∴∠A2OE=45°,∴α=∠A1OA2=90°-40°+90°+45°=185°,
此时∠EOB2=15°,
故B2在O点的北偏西75°方向上.
②O在B点的南偏西60°方向.
③B在A点的正东方向.
④A在B点的正西方向;
(2)∵三角板绕O点顺时针旋转40°角,
∴∠AOB1=40°+60°=100°,
∴∠COB1=100°-90°=10°,

∴B1在O点南偏东80°方向;
(3)∠AOA1,∠AOB,∠AOB1,∠A1OB,∠A1OB1,∠BOB1,共6个;
∵三角板绕O点顺时针旋转40°角,
∴∠AOA1=40°,
∴∠AOA1+∠AOB+∠AOB1+∠A1OB+∠A1OB1+∠BOB1=40°+60°+100°+20°+60°+40°=320°;
(4)如图所示:∵点A2在O点的西南方向,
∴∠A2OE=45°,∴α=∠A1OA2=90°-40°+90°+45°=185°,
此时∠EOB2=15°,
故B2在O点的北偏西75°方向上.
点评:此题主要考查了方向角问题以及图形的旋转,结合图形得出旋转后图形是解题关键.

练习册系列答案
相关题目
向上发射一枚炮弹,经x秒后的高度为y,且时间与高度的关系式为y=ax2+bx,若此时炮弹在第7秒与第13秒时的高度相等,则在下列哪一个时间的高度是最高的( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
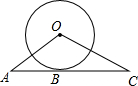 如图,半径为3cm的⊙O与直线AC相切于点B,若AB=
如图,半径为3cm的⊙O与直线AC相切于点B,若AB= 如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.
如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.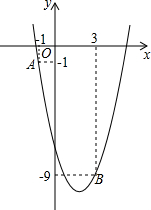 如图,抛物线y=ax2-4x+c经过A(-1,-1)和B(3,-9).
如图,抛物线y=ax2-4x+c经过A(-1,-1)和B(3,-9).