题目内容
 已知:如图,△ABC的外接圆⊙O,弦BC的长为4,∠A=30°,求圆心O到BC的距离.
已知:如图,△ABC的外接圆⊙O,弦BC的长为4,∠A=30°,求圆心O到BC的距离.考点:垂径定理,圆周角定理
专题:
分析:连接OB,OC,过点O作OD⊥BC于点D,先根据圆周角定理判断出△OBC是等边三角形,再由锐角三角函数的定义即可得出结论.
解答: 解:连接OB,OC,过点O作OD⊥BC于点D,
解:连接OB,OC,过点O作OD⊥BC于点D,
∵∠A=30°,
∴∠BOC=60°.
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC=4,
∴OD=OB•sin60°=4×
=2
,即圆心O到BC的距离为2
.
 解:连接OB,OC,过点O作OD⊥BC于点D,
解:连接OB,OC,过点O作OD⊥BC于点D,∵∠A=30°,
∴∠BOC=60°.
∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC=4,
∴OD=OB•sin60°=4×
| ||
| 2 |
| 3 |
| 3 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出等边三角形是解答此题的关键.

练习册系列答案
相关题目
若2x2+1与4x2-2x-5的值互为相反数,则x的值是( )
A、-1或
| ||
B、1或-
| ||
C、1或-
| ||
D、1或
|
 如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.
如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.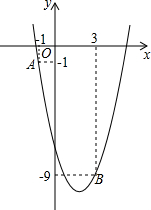 如图,抛物线y=ax2-4x+c经过A(-1,-1)和B(3,-9).
如图,抛物线y=ax2-4x+c经过A(-1,-1)和B(3,-9). 如图,E为正方形ABCD内一点,∠AEB=135°,△AEB按顺时针方向旋转一个角度后成为△CFB,图中
如图,E为正方形ABCD内一点,∠AEB=135°,△AEB按顺时针方向旋转一个角度后成为△CFB,图中 如图,DO⊥AB于,CO⊥EO于O,则∠AOC与∠BOE的关系是
如图,DO⊥AB于,CO⊥EO于O,则∠AOC与∠BOE的关系是