题目内容
15．若A（-$\frac{13}{4}$，y1）、B（-1，y2）、C（$\frac{5}{3}$，y3）为二次函数y=-x2+4x+5的图象上的三点，则y1、y2、y3的大小关系是（ ）| A． | y1＜y2＜y3 | B． | y3＜y2＜y1 | C． | y3＜y1＜y2 | D． | y2＜y1＜y3 |
分析 将二次函数y=-x2+4x+5配方，求对称轴，再根据A、B、C三点与对称轴的位置关系，开口方向判断yl，y2，y3的大小．
解答 解：∵y=-x2+4x+5=-（x-2）2+9，
∴抛物线开口向下，对称轴为x=2，
∵A、B、C三点中，C点离对称轴最近，A点离对称轴最远，
∴y1＜y2＜y3．
故选A．
点评 本题考查了二次函数的增减性．当二次项系数a＞0时，在对称轴的左边，y随x的增大而减小，在对称轴的右边，y随x的增大而增大；a＜0时，在对称轴的左边，y随x的增大而增大，在对称轴的右边，y随x的增大而减小．
练习册系列答案
相关题目
如图，△ABC与△AED中，∠E=∠C，DE=BC，EA=CA，过A作AF⊥DE垂足为F，DE交CB的延长线于点G，连接AG．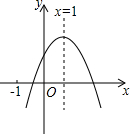
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0②b＜a+c③4a+2b+c＞0④2c＜3b⑤a+b＞m（am+b）（m≠1的实数），其中正确的结论的有（ ）
如图，在△ABC中，AB=10，AC=8，O为△ABC角平分线的交点，若△ABO的面积为20，则△ACO的面积为16．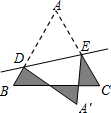
等腰△ABC的腰为6，底为5，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，求阴影部分图形的周长．
如图，已知数轴上的点A表示的数为6，点B表示的数为-4，点C到点A、点B的距离相等，动点P从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t大于0）秒．