题目内容
6. 如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.(1)求证:GA平分∠DGB;
(2)若S四边形DGBA=6,AF=$\frac{3}{2}$,求FG的长.
分析 (1)先过点A作AH⊥BC于H,判定△ABC≌△AED,得出AF=AH,再判定Rt△AFG≌Rt△AHG,即可得出∠AGF=∠AGH;
(2)先判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,再根据Rt△AFG≌Rt△AHG,求得Rt△AFG的面积=3,进而得到FG的长.
解答 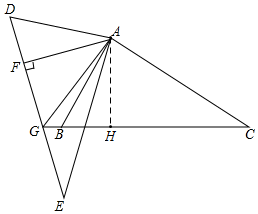 解:(1)过点A作AH⊥BC于H,
解:(1)过点A作AH⊥BC于H,
∵△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,
∴△ABC≌△ADE(SAS),
∴S△ABC=S△AED,
又∵AF⊥DE,
即$\frac{1}{2}$×DE×AF=$\frac{1}{2}$×BC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,AG=AG,
∴Rt△AFG≌Rt△AHG(HL),
∴∠AGF=∠AGH,
即GA平分∠DGB;
(2)∵△ABC≌△ADE,
∴AD=AB,
又∵AF⊥DE,AH⊥BC,AF=AH,
∴Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF=$\frac{3}{2}$,
∴$\frac{1}{2}$×FG×$\frac{3}{2}$=3,
解得FG=4.
点评 本题主要考查了全等三角形的判定与性质,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
15.若A(-$\frac{13}{4}$,y1)、B(-1,y2)、C($\frac{5}{3}$,y3)为二次函数y=-x2+4x+5的图象上的三点,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
16.下列计算结果中等于3的数是( )
| A. | |-7|+|+4| | B. | |(-7)+(+4)| | C. | |+7|+|-4| | D. | |(-7)-(-3)| |
 已知:如图,在△ABC的边BC的同侧,以AB,AC为边向外作等边三角形ABD和等边三角形ACE,连接BE、CD,相交于点M.
已知:如图,在△ABC的边BC的同侧,以AB,AC为边向外作等边三角形ABD和等边三角形ACE,连接BE、CD,相交于点M. 如图所示,AB,CD相交于点O,AE为∠BAD的平分线,CE为∠BCD的平分线.
如图所示,AB,CD相交于点O,AE为∠BAD的平分线,CE为∠BCD的平分线. 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,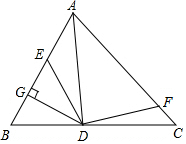 已知:如图所示,在△ABC中,AD是△ABC的角平分线,E、F分别是AB,AC上的点,并且有∠EDF+∠EAF=180°,DG⊥AB于点G.
已知:如图所示,在△ABC中,AD是△ABC的角平分线,E、F分别是AB,AC上的点,并且有∠EDF+∠EAF=180°,DG⊥AB于点G.