Question

7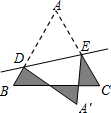．等腰△ABC的腰为6，底为5，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，求阴影部分图形的周长．

Answer 1

分析 根据翻折变换的性质，可得AD=A′D，AE=A′E，然后求出阴影部分的周长等于△ABC的周长，再求解即可．

解答 解：∵△ADE沿DE折叠得到△A′DE，
∴AD=A′D，AE=A′E，
∴A′D+A′E=AD+AE，
∴阴影部分图形的周长等于△ABC的周长，
∵等腰△ABC的腰为6，底为5，
∴等腰△ABC的周长为17，
∴阴影部分图形的周长为17．

点评 本题考查了翻折变换的性质，判断出阴影部分的周长与等边三角形的周长相等是解题的关键．