题目内容
2.计算(1)-32-(5-π)0-|-4|+(-$\frac{1}{3}$)-2
(2)(2×104)3+(-3×106)2-(6×105)3÷(2×10)3
(3)(a+2b)2(a-2b)2
(4)[(2x+y)2-(x+y)(x-4y)-5y2]÷(2x)
分析 (1)根据乘方、零指数幂的运算、绝对值、负指数幂的运算进行计算即可;
(2)根据同底数幂的乘法以及积的乘方进行计算即可;
(3)根据平方差公式和完全平方公式进行计算即可;
(4)根据完全平方公式和平方差公式进行计算即可.
解答 解:(1)原式=-9-1-4+9
=-5;
(2)原式=8×1012+9×1012-216×1015÷8×103
=8×1012+9×1012-27×1012
=-10×1012
=-1013;
(3)原式=[(a+2b)(a-2b)]2
=(a2-4b2)2
=a4-8a2b2+16b4;
(4)原式=[x2+4xy+y2-x2+4xy-xy+4y2-5y2]÷(2x)
=7xy÷2x
=$\frac{7}{2}$y.
点评 本题考查了整式的混合运算,掌握乘方、零指数幂的运算、绝对值、负指数幂的运算、同底数幂的乘法以及积的乘方运算法则、完全平方公式和平方差公式是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
13.射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)完成表中填空①9;②9;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为$\frac{4}{3}$,你认为推荐谁参加比赛更合适,请说明理由.
(注:方差公式s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为$\frac{4}{3}$,你认为推荐谁参加比赛更合适,请说明理由.
(注:方差公式s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
17.下列各式中,最简二次根式是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{4b}$ | D. | $\sqrt{30}$ |
11.将圆心角为90°,面积为4π的扇形围成一个圆锥的一个侧面,所围成圆锥的底面半径为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.将方程-x2-8x=10化为一元二次方程的一般形式,其中二次项系数为1,一次项系数、常数项分别是( )
| A. | -8、-10 | B. | -8、10 | C. | 8、-10 | D. | 8、10 |
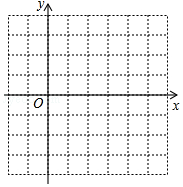 请在网格坐标系中画出二次函数y=x2-4x+1的大致图象(注:图中小正方形网格的边长为1),根据图象填空:
请在网格坐标系中画出二次函数y=x2-4x+1的大致图象(注:图中小正方形网格的边长为1),根据图象填空: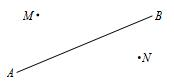 如图,一辆汽车在笔直的公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄,设行驶至点P时,离村庄M最近,汽车行驶到点Q时,离村庄N最近,汽车行驶到点O时,到村庄M、N的距离之和最小,请在图中公路AB上分别画出点P、Q、O的位置,并说明理由.
如图,一辆汽车在笔直的公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄,设行驶至点P时,离村庄M最近,汽车行驶到点Q时,离村庄N最近,汽车行驶到点O时,到村庄M、N的距离之和最小,请在图中公路AB上分别画出点P、Q、O的位置,并说明理由.