题目内容
19.已知二次函数y=$\frac{1}{2}{x^2}$+bx的图象过点A(4,0),设点C(1,-3),在抛物线的对称轴上求一点P,使|PA-PC|的值最大,则点P的坐标为(2,-6).分析 先把A(4,0)代入y=$\frac{1}{2}{x^2}$+bx,求出b的值,得到二次函数解析式,再根据抛物线的对称性求出二次函数y=$\frac{1}{2}{x^2}$-2x与x轴的另一交点是O(0,0),由A、O关于对称轴对称,则可知PA=PO,则当P、O、C三点在一条线上时满足|PA-PC|最大,利用待定系数法可求得直线OC解析式,则可求得P点坐标.
解答 解:∵二次函数y=$\frac{1}{2}{x^2}$+bx的图象过点A(4,0),
∴0=$\frac{1}{2}$×42+4b,解得b=-2,
∴y=$\frac{1}{2}{x^2}$-2x,
∴对称轴为x=$\frac{2}{2×\frac{1}{2}}$=2,
∵二次函数y=$\frac{1}{2}{x^2}$-2x与x轴交于点A(4,0),
∴它与x轴的另一交点是O(0,0),
∵P在对称轴上,
∴PA=PO,
∴|PA-PC|=|PO-PC|≤OC,即当P、O、C三点在一条线上时|PA-PC|的值最大,
设直线OC解析式为y=kx,
∴k=-3,
∴直线OC解析式为y=-3x,
令x=2,可得y=-3×2=-6,
∴存在满足条件的点P,其坐标为(2,-6).
故答案为(2,-6).
点评 本题考查了二次函数的性质,待定系数法求函数的解析式,轴对称的性质等知识.求出二次函数y=$\frac{1}{2}{x^2}$-2x与x轴的另一交点是O(0,0),得出P、O、C三点共线时|PA-PC|的值最大是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
10.下列命题中,真命题的个数有( )
①对角线互相平分的四边形是平行四边形;②两组对角分别相等的四边形是平行四边形;③一组对边平行,另一组对边相等的四边形是平行四边形;④对角线相等的四边形是矩形.
①对角线互相平分的四边形是平行四边形;②两组对角分别相等的四边形是平行四边形;③一组对边平行,另一组对边相等的四边形是平行四边形;④对角线相等的四边形是矩形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.以方程组$\left\{\begin{array}{l}{2x+y=t-1}\\{x-y=2t+7}\end{array}\right.$ 的解x、y分别作为某个点的横、纵坐标,得到一个点(x,y),若点(x,y)在第四象限,则t的取值范围是( )
| A. | -5<t<-2 | B. | t>-2 | C. | -2<t<5 | D. | t>-5 |
11.点P1(-2,y1),点P2(3,y2)是一次函数y=-4x+m图象上的两个点,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1>y2>0 | C. | y1<y2 | D. | y1=y2 |
9.“抛一枚均匀硬币,落地后反面朝上”这一事件是( )
| A. | 随机事件 | B. | 必然事件 | C. | 确定事件 | D. | 不可能事件 |
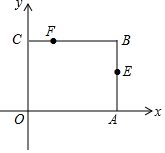 如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.