题目内容
14．抛物线y=（3一k）x2+（k-2）x+2k-1（k≠3）过定点，并求出定点的坐标．分析 根据字母k的系数关系确定定点中的x值，代入后y值是数值，不含有k，此点就是定点．
解答 解：当x=2时，y=4（3一k）+2（k-2）+2k-1，
y=12-4k+2k-4+2k-1，
y=7，
∴定点的坐标为（2，7）．
点评 本题考查了二次函数的字母系数及定点问题，确定定点的横坐标是关键．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
7．
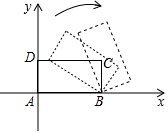已知坐标平面上有一长方形ABCD，其坐标分别为A（0，0），B（2，0），C（2，1），D（0，1），今固定B点并将此长方形依顺时针方向旋转，如图所示．若旋转后C点的坐标为（3，0），则旋转后D点的坐标为何（ ）
已知坐标平面上有一长方形ABCD，其坐标分别为A（0，0），B（2，0），C（2，1），D（0，1），今固定B点并将此长方形依顺时针方向旋转，如图所示．若旋转后C点的坐标为（3，0），则旋转后D点的坐标为何（ ）| A． | （2，2） | B． | （2，3） | C． | （3，3） | D． | （3，2） |
5．已知a=（-2）0，b=（$\frac{1}{2}$）-1，c=（-2）-2，那么a、b、c的大小关系为（ ）
| A． | a＞b＞c | B． | c＞a＞b | C． | c＞b＞a | D． | b＞a＞c |
2．二次根式$\sqrt{{a}^{2}+{b}^{2}}$，$\sqrt{2{b}^{3}}$，$\sqrt{\frac{a}{2}}$，4$\sqrt{3a}$，$\sqrt{8}$，$\sqrt{0.2}$中，最简二次根式有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
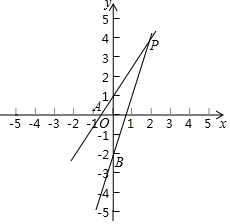已知直线y=$\frac{5}{2}$x+1与y=5x-2的交点为P，两直线分别交y轴于A、B，求△PAB的面积（画图说明）．
如图，图中的几何体是圆柱沿竖直方向切掉一半后得到的，则该几何体的左视图是（ ）
4．若点P在直线y=2x+3上，则点P的坐标可以是（ ）
| A． | （1，5） | B． | （0，2） | C． | （-1，0） | D． | （1，-1） |