题目内容
4.已知一次函数y=-2x+3.(1)分别求这个函数图象与x轴和y轴的交点坐标;
(2)求这个函数图象与两条坐标轴所构成的三角形的面积;
(3)当这个函数图象在x轴下方时,求自变量x的取值范围.
分析 (1)分别把x=0和y=0代入函数的解析式中即可求解;
(2)根据图象与坐标轴的交点坐标即可求出一次函数y=-2x+3与坐标轴围成的三角形面积;
(3)函数的图象位于x轴的下方时,即函数值y小于0,解不等式-2x+3<0即可求出自变量的取值范围.
解答 解:(1)当x=0时,y=3,
当y=0时,x=$\frac{3}{2}$,
则与坐标轴交于点(-$\frac{3}{2}$、0),(0、3);
(2)由(1)知,与坐标轴交于点(-$\frac{3}{2}$、0),(0、3),则这个函数图象与两条坐标轴所构成的三角形的面积=$\frac{1}{2}$×3×$\frac{3}{2}$=$\frac{9}{4}$;
(3)由题意,得-2x+3<0,
解得x>$\frac{3}{2}$.
故当这个函数图象在x轴下方时,自变量x的取值范围是x>$\frac{3}{2}$.
点评 本题考查了一次函数图象上点的坐标特征,求出与x轴的交点坐标、与y轴的交点坐标是解题的关键.

练习册系列答案
相关题目
9.下列运算中正确的是( )
| A. | 3a-a=3 | B. | a2•a3=a6 | C. | (-2a)3=-6a 3 | D. | ab2÷a=b 2 |
16.已知反比例函数y=$\frac{-1}{x}$,下列结论不正确的是( )
| A. | 该函数图象经过点(-1,1) | B. | 该函数图象在第二、四象限 | ||
| C. | 当x<0时,y随着x的增大而减小 | D. | 当x>1时,-1<y<0 |
13.下列函数中,y随x增大而减少的是( )
| A. | y=2x-1 | B. | y=-x+3 | C. | y=$\frac{1}{2}$x+2 | D. | y=2x |
14.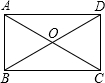 如图,矩形ABCD的两条对角线的一个交角为60o,两条对角线的长度的和为24cm,则这个矩形中AB的长为( )
如图,矩形ABCD的两条对角线的一个交角为60o,两条对角线的长度的和为24cm,则这个矩形中AB的长为( )
 如图,矩形ABCD的两条对角线的一个交角为60o,两条对角线的长度的和为24cm,则这个矩形中AB的长为( )
如图,矩形ABCD的两条对角线的一个交角为60o,两条对角线的长度的和为24cm,则这个矩形中AB的长为( )| A. | 12cm | B. | 8cm | C. | 5cm | D. | 6cm |
 如图,直线y=x+2与抛物线y=$\frac{1}{4}{x}^{2}$+c相交于A、B两点,若∠AOB=45°,则c的值为$\frac{\sqrt{11}}{2}$.
如图,直线y=x+2与抛物线y=$\frac{1}{4}{x}^{2}$+c相交于A、B两点,若∠AOB=45°,则c的值为$\frac{\sqrt{11}}{2}$.