题目内容
13. 如图,平行四边形ABCD中,F是AD边上一点,延长BF、CD交于点E.
如图,平行四边形ABCD中,F是AD边上一点,延长BF、CD交于点E.(1)求证:△ABF∽△DEF;
(2)若$DE=\frac{1}{2}CD$,S△DEF=2,求平行四边形ABCD的面积.
分析 (1)根据平行四边形对角相等可得∠A=∠D,对边平行可得AB∥CD,根据两直线平行,内错角相等得到∠ABF=∠E,然后利用两角对应相等,两三角形相似即可证明.
(2)由$DE=\frac{1}{2}CD$,可知$\frac{DE}{AB}=\frac{1}{2}$,$\frac{DE}{EC}=\frac{1}{3}$,易知△ABF∽△DEF,△CEB∽△DEF,根据相似三角形的面积比等于相似比的平方,求出△ABF和△BCE的面积即可求出平行四边形ABCD的面积.
解答 解:(1)∵四边形ABCD是平行四边形,
∴∠A=∠D,AB∥CD,
∴∠ABF=∠E,
在△ABF和△DEF中,
∠A=∠D,∠ABF=∠E,
∴△ABF∽△CEB.
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△DEF,△CEB∽△DEF,
∵$DE=\frac{1}{2}CD$,
∴$\frac{DE}{AB}=\frac{1}{2}$,$\frac{DE}{EC}=\frac{1}{3}$,
∴$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=$\frac{1}{4}$,$\frac{{S}_{△DEF}}{{S}_{△CEB}}$=$\frac{1}{9}$
∵S△DEF=2,
∴S△ABF=8,S△CEB=18,
∴S四边形BCDF=S△CEB-S△DEF=18-2=16.
∴S平行四边形ABCD=S△ABF+S四边形BCDF=8+16=24.
点评 本题主要考查了平行四边形的性质,相似三角形的判定和性质,熟悉相似三角形的性质和判定是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
8.解方程组$\left\{{\begin{array}{l}{2x-3y=2,…①}\\{2x+y=10.…②}\end{array}}\right.$时,由②-①得( )
| A. | 2y=8 | B. | 4y=8 | C. | -2y=8 | D. | -4y=8 |
3.计算$\sqrt{12}$-$\sqrt{\frac{3}{4}}$的结果正确的是( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{8}$ | D. | 0 |
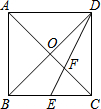 如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$.
如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$. 如图,△ABC中,CD⊥AB于D,下列条件中,能证明△ABC是直角三角形的有①②④.(在横线上填上你认为所有正确答案的序号)
如图,△ABC中,CD⊥AB于D,下列条件中,能证明△ABC是直角三角形的有①②④.(在横线上填上你认为所有正确答案的序号)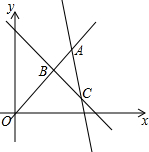 已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.
已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.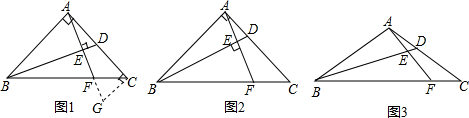
 如图,CD平分∠ACB,且CD∥AE,如果∠ACE=80°.求∠CAE.
如图,CD平分∠ACB,且CD∥AE,如果∠ACE=80°.求∠CAE.