题目内容
16.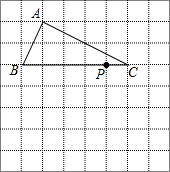 如图,将三角形ABC放在每个小正方形的边长为1的网格中,点A,点B,点C,点P均落在格点上.
如图,将三角形ABC放在每个小正方形的边长为1的网格中,点A,点B,点C,点P均落在格点上.(1)计算三角形ABC的周长等于3$\sqrt{5}$+5.
(2)请在给定的网格内作三角形ABC的内接矩形EFGH,使得点E,H分别在边AB,AC上,点F,G在边BC上,且使矩形EFGH的周长等于线段BP长度的2倍,并简要说明你的作图方法(不要求证明)
分析 (1)根据勾股定理分别求出AB、AC即可解决问题.
(2)在线段AB上截取BE=$\frac{1}{3}$AB,作EF⊥BC于F,EH∥BC交AC于H,作HG⊥BC于G,矩形EFGH计算所求作的矩形.作AM⊥BC于M,交EH于N,设EF=x,则MN=EF=x,
由△AEH∽△ABC,得$\frac{EH}{BC}$=$\frac{AN}{AM}$,列出方程即可解决.
解答 解:(1)∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BC=5,
∴AB+AC+BC=3$\sqrt{5}$+5,
∴△ABC的周长为3$\sqrt{5}$+5.
故答案为3$\sqrt{5}$+5.
(2)在线段AB上截取BE=$\frac{1}{3}$AB,作EF⊥BC于F,EH∥BC交AC于H,作HG⊥BC于G,矩形EFGH计算所求作的矩形.
理由:作AM⊥BC于M,交EH于N,设EF=x,则MN=EF=x,
∵矩形EFGH的周长为8,
∴EH=4-x,
∵EH∥BC,
∴△AEH∽△ABC,
∴$\frac{EH}{BC}$=$\frac{AN}{AM}$,
∴$\frac{2-x}{2}=\frac{4-x}{5}$,
∴x=$\frac{2}{3}$,
∴EF=$\frac{2}{3}$,
∵EF∥AM,
∴$\frac{BE}{BA}$=$\frac{EF}{AM}$=$\frac{\frac{2}{3}}{2}$=$\frac{1}{3}$,
∴BE=$\frac{1}{3}$AB,
∴当BE=$\frac{1}{3}$AB时,矩形EFGH的周长等于线段BP长度的2倍.
点评 本题考查矩形性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是先利用相似三角形的性质求出矩形的长、宽,然后确定点E位置,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案 下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是( )
下图是某中学的平面示意图,每个正方形格子的边长为1,如果校门所在位置的坐标为(2,4),小明所在位置的坐标为(-6,-1),那么坐标(3,-2)在示意图中表示的是( )| A. | 图书馆 | B. | 教学楼 | C. | 实验楼 | D. | 食堂 |
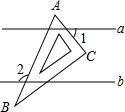 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
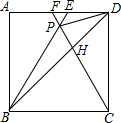 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论: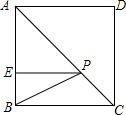 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.
如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.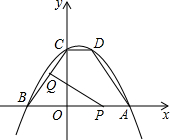 如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.
如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.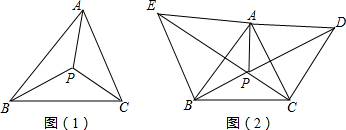
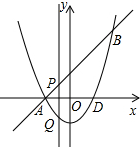 如图,抛物线与直线相交于A,B两点,若点A在x轴上,点B的坐标是(2,4),抛物线与x轴另一交点为D,并且△ABD的面积为6,直线AB与y轴的交点的坐标为(0,2).点P是线段AB(不与A,B重合)上的一个动点,过点P作x轴的垂线,交抛物线与点Q.
如图,抛物线与直线相交于A,B两点,若点A在x轴上,点B的坐标是(2,4),抛物线与x轴另一交点为D,并且△ABD的面积为6,直线AB与y轴的交点的坐标为(0,2).点P是线段AB(不与A,B重合)上的一个动点,过点P作x轴的垂线,交抛物线与点Q.