题目内容
15．已知关于x的一元二次方程x2-（2m-4）x+m2-4m+3=0．（1）求证：不论m取何值，方程都有两个不相等的实数根；
（2）若原方程的两个实数根一个小于2，另一个大于2，求m的取值范围．
分析 （1）要证明方程总有两个不相等的实数根就是证明其判别式永远都是一个正数；
（2）先求出原方程的两个实数根，根据两个实数根一个大于2，另一个小于2，列出不等式组，求出m的取值范围．
解答 （1）证明：∵△=[-（2m-4）]2-4（m2-4m+3）=4m2-16m+16-4m2+16m-12=4＞0，
∴不论m取何值，方程都有两个不相等实数根；
（2）解：∵x2-（2m-4）x+m2-4m+3=0，
∴（x-m+1）（x-m+3）=0，
∴x1=m-1，x2=m-3．
则由题意，得$\left\{\begin{array}{l}{m-1＞2}\\{m-3＜2}\end{array}\right.$，
解得3＜m＜5．
即m的取值范围是3＜m＜5．
点评 本题考查一元二次方程根的判别式，△＞0?方程有两个不相等的实数根；△=0?方程有两个相等的实数根；△＜0?方程没有实数根．同时考查了因式分解法解一元二次方程及解一元一次不等式组．
练习册系列答案
相关题目
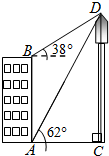某校一大楼AB的高为18米，不远处有一水塔CD．某同学在楼底A处测得塔顶D处的仰角为62°，在楼顶B点测得塔顶D处仰角为38°．求CD的高度（结果精确到0.1米）（ 参考数据：sin62°≈0.88，cos62°≈0.47，tan62°≈1.88，sin38°≈0.62，cos38°≈0.79，tan38°≈0.78）