题目内容
20．已知x2-3x-4=0，x≠0，则x2+$\frac{16}{{x}^{2}}$=17；（x-$\frac{4}{x}$）2=9；$\frac{{x}^{4}}{{x}^{8}+2{x}^{4}+256}$=$\frac{1}{259}$．分析 在已知x2-3x-4=0中，方程两边同时除以x，求得x-$\frac{4}{x}$的值，则（x-$\frac{4}{x}$）2即可求解，利用完全平方公式即可求得x2+$\frac{16}{{x}^{2}}$的值，$\frac{{x}^{4}}{{x}^{8}+2{x}^{4}+256}$=$\frac{\frac{{x}^{4}}{{x}^{4}}}{\frac{{x}^{8}}{{x}^{4}}+\frac{2{x}^{4}}{{x}^{4}}+\frac{256}{{x}^{4}}}$=$\frac{1}{（{x}^{2}+\frac{16}{{x}^{2}}）^{2}-32+2}$，然后代入求解即可．
解答 解：∵x2-3x-4=0，
∴x-$\frac{4}{x}$=3，
∴（x-$\frac{4}{x}$）2=9，
∴x2+$\frac{16}{{x}^{2}}$=17；
$\frac{{x}^{4}}{{x}^{8}+2{x}^{4}+256}$=$\frac{\frac{{x}^{4}}{{x}^{4}}}{\frac{{x}^{8}}{{x}^{4}}+\frac{2{x}^{4}}{{x}^{4}}+\frac{256}{{x}^{4}}}$=$\frac{1}{{x}^{4}+2+\frac{256}{{x}^{4}}}$=$\frac{1}{（{x}^{2}+\frac{16}{{x}^{2}}）^{2}-32+2}$=$\frac{1}{1{7}^{2}-32+2}$=$\frac{1}{259}$．
故答案是：17，9，$\frac{1}{259}$．
点评 此题主要考查了完全平方公式以及分式的混合运算，正确应用完全平方公式是解题关键．
千里马走向假期期末仿真试卷寒假系列答案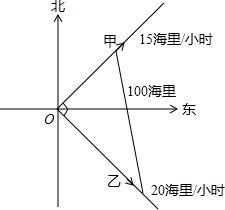
两条船同时从A港出发，一艘船的速度是15海里/时，航向是东北方向，另一艘船比它每小时快5海里，航向是东南方向，多少小时后两船相距100海里？