题目内容
已知关于x的一次函数y=(2m-4)x+m-2,若这个函数的图象与y轴负半轴相交,且与两个坐标围成的三角形面积为
.
(1)求这个函数的解析式;
(2)求直线y=-x和(1)中函数的图象与x轴围成的三角形面积.
| 1 |
| 2 |
(1)求这个函数的解析式;
(2)求直线y=-x和(1)中函数的图象与x轴围成的三角形面积.
考点:待定系数法求一次函数解析式,两条直线相交或平行问题
专题:计算题
分析:(1)由于函数的图象与y轴负半轴相交,则m-2<0,解得m<2,再确定一次函数y=(2m-4)x+m-2与x轴的交点坐标为(-
,0),利用三角形面积公式得到
×
×[-(m-2)]=
,解得m=0,于是得到这个函数的解析式为y=-4x-2;
(2)先解方程组
得直线y=-8x-4与y=-x的交点坐标为(-
,
),然后根据三角形面积公式计算直线y=-8x-4和y=-x与x轴围成的三角形面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)先解方程组
|
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:(1)根据题意m-2<0,解得m<2,
把y=0代入y=(2m-4)x+m-2得x=-
,
∴一次函数y=(2m-4)x+m-2与y轴的交点坐标为(0,m-2),与x轴的交点坐标为(-
,0),
∵一次函数y=(2m-4)x+m-2与两个坐标围成的三角形面积为
,
∴
×
×[-(m-2)]=
,
解得m=0,
∴这个函数的解析式为y=-4x-2;
(2)解方程组
得
,
∴直线y=-8x-4与y=-x的交点坐标为(-
,
),
∴直线y=-8x-4和y=-x与x轴围成的三角形面积=
×
×
=
.
把y=0代入y=(2m-4)x+m-2得x=-
| 1 |
| 2 |
∴一次函数y=(2m-4)x+m-2与y轴的交点坐标为(0,m-2),与x轴的交点坐标为(-
| 1 |
| 2 |
∵一次函数y=(2m-4)x+m-2与两个坐标围成的三角形面积为
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得m=0,
∴这个函数的解析式为y=-4x-2;
(2)解方程组
|
|
∴直线y=-8x-4与y=-x的交点坐标为(-
| 2 |
| 3 |
| 2 |
| 3 |
∴直线y=-8x-4和y=-x与x轴围成的三角形面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |
点评:本题考查了待定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将点的坐标代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
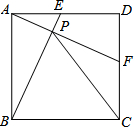 如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:
如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究: 我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=
我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y= 任意抛掷一枚均匀的骰子(各个面上的点数为1-6),将第一次,第二次抛掷的点数分别记为m,n
任意抛掷一枚均匀的骰子(各个面上的点数为1-6),将第一次,第二次抛掷的点数分别记为m,n 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为