Question

6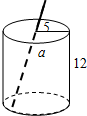．如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，已知一条到达底部的直吸管在罐内部分的长度为a，若直吸管在罐外部分还剩余3，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是（　　）

• A． 12≤b≤13
• B． 12≤b≤15
• C． 13≤b≤16
• D． 15≤b≤16

Answer 1

分析 如图，当吸管底部在O点时吸管在罐内部分a最短，此时a就是圆柱形的高；当吸管底部在A点时吸管在罐内部分a最长，此时a可以利用勾股定理在Rt△ABO中即可求出，进而得出答案．

解答 解：如图，连接BO，AO，
当吸管底部在O点时吸管在罐内部分a最短，
此时a就是圆柱形的高，
即a=12；
当吸管底部在A点时吸管在罐内部分a最长，
即线段AB的长，
在Rt△ABO中，
AB=$\sqrt{A{O}^{2}+B{O}^{2}}$
=$\sqrt{{5}^{2}+1{2}^{2}}$
=13，
故此时a=13，
所以12≤a≤13，
则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是：15≤b≤16．
故选：D．

点评 本题考查了勾股定理的应用，善于观察题目的信息，正确理解题意是解题的关键．