题目内容
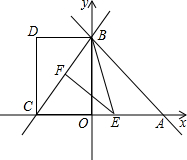
 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为考点:正方形的性质,一次函数图象上点的坐标特征
专题:压轴题,规律型
分析:根据直线解析式判断出直线与x轴的夹角为45°,从而得到直线与正方形的边围成的三角形是等腰直角三角形,再根据点A的坐标求出正方形的边长并得到变化规律表示出第n个正方形的边长,然后根据阴影部分的面积等于一个等腰直角三角形的面积加上梯形的面积再减去一个直角三角形的面积列式求解并根据结果的规律解答即可.
解答:解:∵函数y=x与x轴的夹角为45°,
∴直线y=x与正方形的边围成的三角形是等腰直角三角形,
∵A(8,4),
∴第四个正方形的边长为8,
第三个正方形的边长为4,
第二个正方形的边长为2,
第一个正方形的边长为1,
…,
第n个正方形的边长为2n-1,
由图可知,S1=
×1×1+
×(1+2)×2-
×(1+2)×2=
,
S2=
×4×4+
×(4+8)×8-
×(4+8)×8=8,
…,
Sn为第2n与第2n-1个正方形中的阴影部分,
第2n个正方形的边长为22n-1,第2n-1个正方形的边长为22n-2,
Sn=
•22n-2•22n-2=24n-5.
故答案为:24n-5.

∴直线y=x与正方形的边围成的三角形是等腰直角三角形,
∵A(8,4),
∴第四个正方形的边长为8,
第三个正方形的边长为4,
第二个正方形的边长为2,
第一个正方形的边长为1,
…,
第n个正方形的边长为2n-1,
由图可知,S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
…,
Sn为第2n与第2n-1个正方形中的阴影部分,
第2n个正方形的边长为22n-1,第2n-1个正方形的边长为22n-2,
Sn=
| 1 |
| 2 |
故答案为:24n-5.
点评:本题考查了正方形的性质,三角形的面积,一次函数图象上点的坐标特征,依次求出各正方形的边长是解题的关键,难点在于求出阴影Sn所在的正方形和正方形的边长.

练习册系列答案
相关题目
 如图,在平面直角坐标系xoy中,直线
如图,在平面直角坐标系xoy中,直线 如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设
如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设 如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB=
如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB=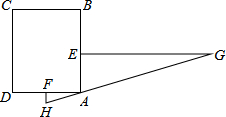 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH= 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1: 如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.
如图,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EF⊥AC,分别交AC于点E,CB的延长线于点F.