题目内容
8.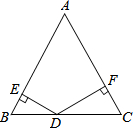 如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若△ABC的BC边上的高为2,则DE2+2DE•DF+DF2=4.
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若△ABC的BC边上的高为2,则DE2+2DE•DF+DF2=4.
分析 作AG⊥BC于G,根据等边三角形的性质得出∠B=60°,解直角三角形求得AG=2,根据S△ABD+S△ACD=S△ABC即可得出DE+DF=AG=2cm.
解答 解:作AG⊥BC于G,
∵△ABC是等边三角形,
∴∠B=60°,
∴AG=2cm,
连接AD,
∵S△ABD+S△ACD=S△ABC,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$BC•AG,
∵AB=AC=BC=2,
∴DE+DF=AG=2cm,
∴DE2+2DE•DF+DF2=(DE+DF)2=4,
故答案为4
点评 本题考查了等边三角形的性质,解直角三角函数以及三角形面积等,根据S△ABD+S△ACD=S△ABC即可得出DE+DF=AG是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列说法错误的是( )
| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 若两条直线相交所成的角是直角,则这两条直线互相垂直 |
 如图,已知等边△ABC内接于⊙O,AB=2,则△ABC的外接圆半径为$\frac{2\sqrt{3}}{3}$cm.
如图,已知等边△ABC内接于⊙O,AB=2,则△ABC的外接圆半径为$\frac{2\sqrt{3}}{3}$cm.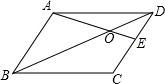 如图,在?ABCD中,E为CD中点,AE交BD于点O,S△AOB=12cm2,则S△EOD=3cm2.
如图,在?ABCD中,E为CD中点,AE交BD于点O,S△AOB=12cm2,则S△EOD=3cm2. 如图,AB∥CD,∠BAE=135°,∠DCE=40°,则∠AEC=85度.
如图,AB∥CD,∠BAE=135°,∠DCE=40°,则∠AEC=85度.
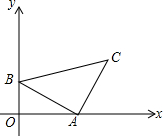 如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).
如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).