题目内容
18. 如图,已知等边△ABC内接于⊙O,AB=2,则△ABC的外接圆半径为$\frac{2\sqrt{3}}{3}$cm.
如图,已知等边△ABC内接于⊙O,AB=2,则△ABC的外接圆半径为$\frac{2\sqrt{3}}{3}$cm.
分析 作直径AD,连接BD,根据等边三角形性质求出∠C=60°,根据圆周角定理求出∠D=∠C=60°,解直角三角形求出AD即可.
解答  解:如图,作直径AD,连接BD,
解:如图,作直径AD,连接BD,
∵等边△ABC内接于⊙O,AD为直径,
∴∠C=60°=∠D,∠ABD=90°,
∵sin∠D=$\frac{AB}{AD}$=$\frac{\sqrt{3}}{2}$,
∴AD=$\frac{2AB}{\sqrt{3}}$=$\frac{2×2}{\sqrt{3}}$=$\frac{4}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$cm,
∴⊙0的半径是$\frac{2\sqrt{3}}{3}$cm.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查的是三角形的外接圆与外心,涉及到等边三角形的性质,圆周角定理,解直角三角形的应用,关键是能正确作出辅助线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.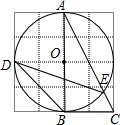 如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )
如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )
 如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )
如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
7.一艘轮船在甲、乙两地之间航行,已知水流速度是5千米/小时,顺水航行需要6小时,逆水航行需要8小时,则甲乙两地间的距离是( )
| A. | 220千米 | B. | 240千米 | C. | 260千米 | D. | 350千米 |
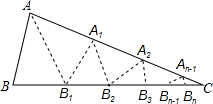 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.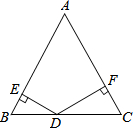 如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若△ABC的BC边上的高为2,则DE2+2DE•DF+DF2=4.
如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若△ABC的BC边上的高为2,则DE2+2DE•DF+DF2=4.