题目内容
3．
如图，AB∥CD，∠BAE=135°，∠DCE=40°，则∠AEC=85度．
分析 过点E作EF∥AB，根据平行公理可得EF∥CD，再根据两直线平行，同旁内角互补求出∠AEF，再根据两直线平行，内错角相等求出∠CEF，然后根据∠AEC=∠AEF+∠CEF计算即可得解．
解答 
解：如图，过点E作EF∥AB，
所以∠AEF=180°-∠A=180°-135°=45°，
由平行公理得EF∥CD，
所以∠CEF=∠DCE=40°，
所以∠AEC=∠AEF+∠CEF=45°+40°=85°．
故答案为：85．
点评 本题考查了平行线的性质，熟记性质是解题的关键，此类题目，难点在于过拐点作辅助线．
练习册系列答案
口算能手系列答案
相关题目
13．
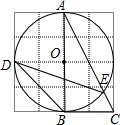如图，边长为1的小正方形构成的网格中，半径为2的⊙O的圆心O在格点上，则∠BDE的正切值等于（ ）
如图，边长为1的小正方形构成的网格中，半径为2的⊙O的圆心O在格点上，则∠BDE的正切值等于（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{1}{2}$ | D． | 2 |
11．2011年成都市大约有3万名学生参加中考，为了考查他们的数学考试情况，评卷人抽取了1000名学生的数学成绩进行统计，那么下列四个判断正确的是（ ）
| A． | 每名学生的数学成绩是个体 | B． | 3万名学生是总体 | ||
| C． | 上述调查是普查 | D． | 1000名考生是总体的一个样本 |
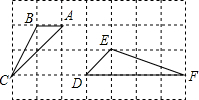如图，方格纸中每个小正方形的边长都为1，△ABC和△DEF的顶点都在方格纸的格点上．则可判断△ABC和△DEF是否相似：相似（请填“相似”或“不相似”）
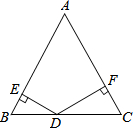如图，△ABC是等边三角形，点D是BC边上任意一点，DE⊥AB于点E，DF⊥AC于点F，若△ABC的BC边上的高为2，则DE2+2DE•DF+DF2=4．
15．不等式$\frac{x}{3}$＞5的解集是（ ）
| A． | x＜$\frac{5}{3}$ | B． | x＞$\frac{5}{3}$ | C． | x＜15 | D． | x＞15 |
12．在圆柱、正方体、长方体中，主视图可能一样的是（ ）
| A． | 仅圆柱和正方体 | B． | 仅圆柱和长方体 | ||
| C． | 仅正方体和长方体 | D． | 圆柱、正方体和长方体 |
