题目内容
18.计算:(1)($\frac{3}{2}\sqrt{5}$-$\sqrt{12}$)$÷\frac{1}{2}\sqrt{3}$
(2)$\sqrt{32}$-$(2+\sqrt{2})^{2}$
(3)$\frac{2}{1-\sqrt{2}}$+$\sqrt{18}$+4$\sqrt{\frac{1}{2}}$
(4)($\sqrt{28}$+5$\sqrt{2}$)($\sqrt{50}$-2$\sqrt{7}$)
分析 (1)先根据二次根式的除法法则运算,然后化简后合并即可;
(2)先利用完全平方公式计算,然后化简后合并即可;
(3)先把二次根式化为最简二次根式,然后合并即可;
(4)先把二次根式化为最简二次根式,然后利用平方差公式计算.
解答 解:(1)原式=$\frac{3}{2}$×2×$\sqrt{5×\frac{1}{3}}$-2$\sqrt{12×\frac{1}{3}}$
=$\sqrt{15}$-4;
(2)原式=4$\sqrt{2}$-(4+4$\sqrt{2}$+2)
=4$\sqrt{2}$-6-4$\sqrt{2}$
=-6;
(3)原式=-2(1+$\sqrt{2}$)+3$\sqrt{2}$+2$\sqrt{2}$
=-2-2$\sqrt{2}$+3$\sqrt{2}$-2$\sqrt{2}$
=3$\sqrt{2}$-2;
(4)原式=(2$\sqrt{7}$+5$\sqrt{2}$)(5$\sqrt{2}$-2$\sqrt{7}$)
=(5$\sqrt{2}$)2-(2$\sqrt{7}$)2
=50-28
=22.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
17. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )
如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )
 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )
如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4$\sqrt{3}$且∠AFG=60°,GE=2BG,则折痕EF的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
9.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | a4•a3=a7 | C. | (a3)2=a5 | D. | (2a)3=6a3 |
8.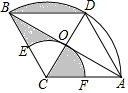 如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )
如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )
 如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )
如图,菱形ACBD中,AB与CD交于点O,∠ACB=120°,以C为圆心、AC为半径作弧AB,再以C为圆心,CO为半径作弧EF分别交AC于点F、BC于点E,若CB=2,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{3}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | π-$\sqrt{3}$ |
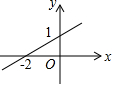 如图,一次函数y=kx+b(k>0)的图象与x轴的交点坐标为(-2,0),与y轴的交点坐标为(0,1),则关于x的不等式kx+b<0的解集是x<-2.
如图,一次函数y=kx+b(k>0)的图象与x轴的交点坐标为(-2,0),与y轴的交点坐标为(0,1),则关于x的不等式kx+b<0的解集是x<-2.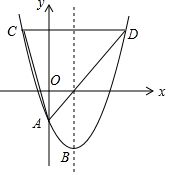 如图,在平面直角坐标系中,抛物线y=a(x-2)2-4与y轴交于点A,顶点为B,点A的坐标为(0,-2),点C在抛物线上(不与点A,B重合),过点C作y轴的垂线交抛物线于点D,连结AC,AD,CD,设点C的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-2)2-4与y轴交于点A,顶点为B,点A的坐标为(0,-2),点C在抛物线上(不与点A,B重合),过点C作y轴的垂线交抛物线于点D,连结AC,AD,CD,设点C的横坐标为m.