题目内容
10．在平面直角坐标系中，?ABCD的顶点A、B、D的坐标分别是（0，0），（5，0），（2，3），且AD∥BC，AB∥CD则顶点C的坐标是（7，3）．分析 根据平行四边形两边分别平行且相等的性质即可得出答案．
解答 解：∵四边形ABCD是平行四边形，点A、B、D的坐标分别是（0，0），（5，0），（2，3），AD∥BC，AB∥CD，
∴CD=AB=5，
∴点C的坐标是（7，3）；
故答案为：（7，3）．
点评 本题主要考查点的坐标、平行四边形的性质；熟练掌握平行四边形的性质是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在△ABC中，DE是AC的垂直平分线，△ABC的周长为27cm，△BCE的周长为18cm，则AD的长为4.5cm．
如图是小凡同学在体育课上跳远后留下的脚印，他的跳远成绩是线段BN的长度，这样测量的依据是垂线段最短．
2．已知23×42=2n，则n的值为（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
19．
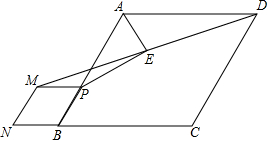如图，在菱形ABCD中，tan∠ABC=$\frac{4}{3}$，P为AB上一点，以PB为边向外作菱形PMNB，连结DM，取DM中点E，连结AE，PE，则$\frac{AE}{PE}$的值为（ ）
如图，在菱形ABCD中，tan∠ABC=$\frac{4}{3}$，P为AB上一点，以PB为边向外作菱形PMNB，连结DM，取DM中点E，连结AE，PE，则$\frac{AE}{PE}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |