��Ŀ����
8��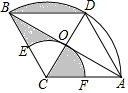 ��ͼ������ACBD�У�AB��CD���ڵ�O����ACB=120�㣬��CΪԲ�ġ�ACΪ�뾶����AB������CΪԲ�ģ�COΪ�뾶����EF�ֱ�AC�ڵ�F��BC�ڵ�E����CB=2����ͼ����Ӱ���ֵ����Ϊ��������
��ͼ������ACBD�У�AB��CD���ڵ�O����ACB=120�㣬��CΪԲ�ġ�ACΪ�뾶����AB������CΪԲ�ģ�COΪ�뾶����EF�ֱ�AC�ڵ�F��BC�ڵ�E����CB=2����ͼ����Ӱ���ֵ����Ϊ��������| A�� | $\frac{2��}{3}$-$\frac{\sqrt{3}}{2}$ | B�� | $\frac{��}{3}$-$\frac{1}{2}$ | C�� | $\frac{2��}{3}$-$\frac{1}{2}$ | D�� | ��-$\sqrt{3}$ |
���� �������ε����ʵõ���BCD=��CBD=60�㣬AB��CD����á�DBO=30�㣬OD=1��OB=$\sqrt{3}$���������κ������ε������ʽ���ɵõ����ۣ�
��� �⣺���ı���ACBD�����Σ���ACB=120�㣬
���BCD=��CBD=60�㣬AB��CD��
���DBO=30�㣬OD=1��OB=$\sqrt{3}$��
��ͼ����Ӱ���ֵ����=$\frac{60•�С�{2}^{2}}{360}$-$\frac{1}{2}$��1��$\sqrt{3}$=$\frac{2}{3}$��-$\frac{\sqrt{3}}{2}$��
��ѡA��
���� ���⿼�������ε����ʣ����ε�����ļ��㣬��ȷ��ʶ��ͼ���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
�����Ŀ
19��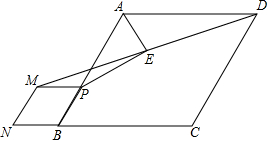 ��ͼ��������ABCD�У�tan��ABC=$\frac{4}{3}$��PΪAB��һ�㣬��PBΪ������������PMNB������DM��ȡDM�е�E������AE��PE����$\frac{AE}{PE}$��ֵΪ��������
��ͼ��������ABCD�У�tan��ABC=$\frac{4}{3}$��PΪAB��һ�㣬��PBΪ������������PMNB������DM��ȡDM�е�E������AE��PE����$\frac{AE}{PE}$��ֵΪ��������
 ��ͼ��������ABCD�У�tan��ABC=$\frac{4}{3}$��PΪAB��һ�㣬��PBΪ������������PMNB������DM��ȡDM�е�E������AE��PE����$\frac{AE}{PE}$��ֵΪ��������
��ͼ��������ABCD�У�tan��ABC=$\frac{4}{3}$��PΪAB��һ�㣬��PBΪ������������PMNB������DM��ȡDM�е�E������AE��PE����$\frac{AE}{PE}$��ֵΪ��������| A�� | $\frac{2}{3}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{3}{4}$ |
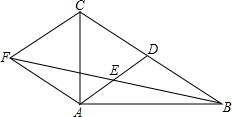 ��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ�E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ����ڵ�F������CF��
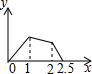
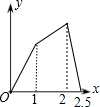
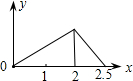
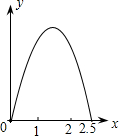
��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ�E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ����ڵ�F������CF��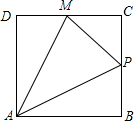 ��ͼ���ڱ߳�Ϊ1��������ABCD�ı�����һ��P��A��B��C��M��˳���˶���M�DZ�CD�ϵ��е㣬���P������·��xΪ�Ա�������APM�����Ϊy�������Ĵ���ͼ���ǣ�������
��ͼ���ڱ߳�Ϊ1��������ABCD�ı�����һ��P��A��B��C��M��˳���˶���M�DZ�CD�ϵ��е㣬���P������·��xΪ�Ա�������APM�����Ϊy�������Ĵ���ͼ���ǣ�������