题目内容
11. 如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
分析 (1)作AM⊥BC于M,由已知条件得出AB=AC,由等腰三角形的性质得出BM=CM,由直角三角形斜边上的中线性质得出AM=$\frac{1}{2}$BC=5,证出△APN和△CEN是等腰直角三角形,得出PN=AP=t,CE=NE=5-t,由CE=CQ-QE=2t-2得出方程,解方程即可;
(2)由平行四边形的判定得出AP=BE,得出方程,解方程即可.
解答 解:(1)作AM⊥BC于M,如图所示: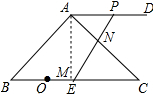
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,
∴AB=AC,
∴BM=CM,
∴AM=$\frac{1}{2}$BC=5,
∵AD∥BC,
∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5-t,
∵CE=CQ-QE=2t-2,
∴5-t=2t-2,
解得:t=$\frac{7}{3}$,sy5BQ=BC-CQ=10-2×$\frac{7}{3}$=$\frac{16}{3}$;
(2)存在,t=4;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10-2t+2,
解得:t=4,
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4.
点评 本题考查了平行四边形的判定、等腰直角三角形的判定与性质、等腰三角形的性质等知识;根据题意得出t的方程是解决问题的突破口.

练习册系列答案
相关题目
1.下列关于方程x2+x-1=0的说法中正确的是( )
| A. | 该方程有两个相等的实数根 | |
| B. | 该方程有两个不相等的实数根,且它们互为相反数 | |
| C. | 该方程有一根为$\frac{{1+\sqrt{5}}}{2}$ | |
| D. | 该方程有一根恰为黄金比例 |
6.将多项式(2x+y)2-(x-2y)2分解因式的正确结果是( )
| A. | (3x+y)(x-3y) | B. | (3x-y)(x+3y) | C. | (3x-y)(x-3y) | D. | (3x+y)(x+3y) |
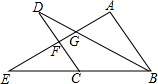 如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.
如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.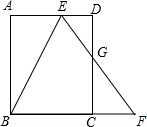 如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.
如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.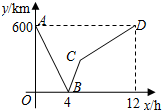 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: