题目内容
2.Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线l的垂线BD、CE,垂足分别为D、E,若BD=3,CE=2,则DE=5.分析 首先证明∠DBA=∠CAE,然后再根据AAS定理证明△BDA≌△AEC,根据全等三角形的性质可得DA=CE,AE=DB,进而得到答案.
解答 解:如图,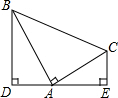
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥DE,
∴∠BDA=90°,
∴∠BAD+∠DBA=90°,
∴∠DBA=∠CAE,
∵CE⊥DE,
∴∠E=90°,
在△BDA和△AEC中,
$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠D=∠E}\\{AB=AC}\end{array}\right.$,
∴△BDA≌△AEC(AAS),
∴DA=CE=2,AE=DB=3,
∴ED=5.
故答案为:5.
点评 此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定定理与性质定理.

练习册系列答案
相关题目
 已知:如图AB=CD,DA⊥CA,AC⊥BC.求证:△ADC≌△CBA.
已知:如图AB=CD,DA⊥CA,AC⊥BC.求证:△ADC≌△CBA. 如图,△ABC中,AB=AC,E为AC上一点,且AE=BE,CE=CB,则∠C=$\frac{540}{7}$度.
如图,△ABC中,AB=AC,E为AC上一点,且AE=BE,CE=CB,则∠C=$\frac{540}{7}$度. 抛物线的部分图象如图所示,则当y<0时,x的取值范围是x>3或x<-1.
抛物线的部分图象如图所示,则当y<0时,x的取值范围是x>3或x<-1.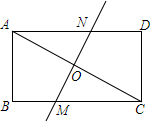 如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.
如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.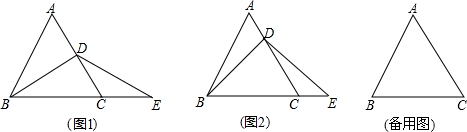
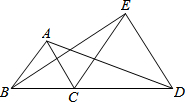 已知,△ABC和△CDE都是等边三角形,
已知,△ABC和△CDE都是等边三角形, 小明家计划靠墙围成一个矩形的小私家花园,如图所示,他家的材料可以使围成的花园总长度为80m,怎样用x表示花园的面积?当x由小到大变化时,花园的总面积怎样发生变化?你能找出使花园的面积最大的x值吗?
小明家计划靠墙围成一个矩形的小私家花园,如图所示,他家的材料可以使围成的花园总长度为80m,怎样用x表示花园的面积?当x由小到大变化时,花园的总面积怎样发生变化?你能找出使花园的面积最大的x值吗?