题目内容
13. 如图,△ABC中,AB=AC,E为AC上一点,且AE=BE,CE=CB,则∠C=$\frac{540}{7}$度.
如图,△ABC中,AB=AC,E为AC上一点,且AE=BE,CE=CB,则∠C=$\frac{540}{7}$度.
分析 根据等腰三角形的性质得到∠ABC=∠C,∠ABE=∠A,∠EBC=∠BEC,由外角的性质得到∠BEC=∠A+∠ABE=2∠A,推出∠EBC=2∠A,于是得到∠ABC=∠C=3∠A,根据三角形的内角和列方程即可得到结论.
解答 解:∵AB=AC,
∴∠ABC=∠C,
∵AE=BE,
∴∠ABE=∠A,
∵CE=CB,
∴∠EBC=∠BEC,
∵∠BEC=∠A+∠ABE=2∠A,
∴∠EBC=2∠A,
∴∠ABC=∠C=3∠A,
∵∠A+∠ABC+∠C=180°,
∴3∠A+3∠A+∠A=180°,
∴∠A=$\frac{180°}{7}$,
∴∠C=$\frac{540°}{7}$,
故答案为:$\frac{540}{7}$.
点评 本题考查了等腰三角形的性质,三角形的内角和,外角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
1. 如图是一个长方体的表面展开图,在原长方体中“南”字所在的面的对面标的字是( )
如图是一个长方体的表面展开图,在原长方体中“南”字所在的面的对面标的字是( )
 如图是一个长方体的表面展开图,在原长方体中“南”字所在的面的对面标的字是( )
如图是一个长方体的表面展开图,在原长方体中“南”字所在的面的对面标的字是( )| A. | 我 | B. | 爱 | C. | 融 | D. | 侨 |




 数学课上,小林同学用n个小立方块搭成一个几何体,从三个方向看到的图形如图所示,则n的值是7.
数学课上,小林同学用n个小立方块搭成一个几何体,从三个方向看到的图形如图所示,则n的值是7.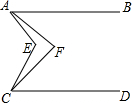 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,则∠AEC=$\frac{4}{3}$∠AFC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,则∠AEC=$\frac{4}{3}$∠AFC.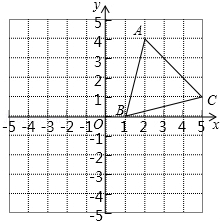 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).