题目内容
13．
如图，在方格纸中，每个小正方形的边长均为1，△ABC的顶点A、B、C均在小正方形的顶点上．（1）在方格纸中，将△ABC绕着点C顺时针旋转90°得到△DEC（点A的对应点为点D，点B的对应点为点E），画出△DEC；
（2）在（1）条件下，在方格纸中画出以A、D、E、F为顶点，且以DE为对角线的平行四边形，连接BF，直接写出线段BF的长．
分析 （1）利用网格特点和旋转的性质画出点B和A的对应点D和E，则可得到△DEC；
（2）作DF∥AE，且DF=AE，则四边形AEFD满足条件，然后利用勾股定理计算BF的长．
解答 解：（1）如图，△DEC为所作；
（2）如图，平行四边形AEFD为所作，BF=$\sqrt{{1}^{2}+{5}^{2}}$=$\sqrt{26}$．
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平行四边形的性质．
练习册系列答案
优生乐园系列答案
相关题目
2．某粮仓原有大米132吨，某一周该粮仓大米的进出情况如下表：（当天运进大米8 吨，记作+8吨；当天运出大米15吨，记作-15吨．）
（1）若经过这一周，该粮仓存有大米88吨，求m的值，并说明星期五该粮仓是运进还是运出大米，运进或运出大米多少吨？
（2）若大米进出库的装卸费用为每吨15元，求这一周该粮仓需要支付的装卸总费用．
| 某粮仓大米一周进出情况表（单位：吨） | ||||||
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| -32 | +26 | -23 | -16 | m | +42 | -21 |
（2）若大米进出库的装卸费用为每吨15元，求这一周该粮仓需要支付的装卸总费用．
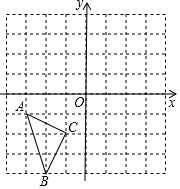△ABC在平面直角坐标系中的位置如图所示