题目内容
13.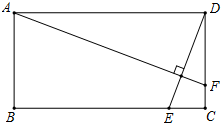 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当CF=1,求EC的长.
分析 (1)易证△ADF∽△DCE,然后运用相似三角形的性质即可得到y与x的关系,然后根据y的范围就可得到x的范围;
(2)由于点F的位置不确定,需分点F在线段DC及点F在线段DC的延长线上两种情况进行讨论,然后利用y与x的关系即可解决问题.
解答 解:(1)∵四边形ABCD是矩形,
∴DC=AB=2,∠ADC=∠BCD=90°.
又∵AF⊥DE,
∴∠ADF=∠DCE=90°,∠DAF=∠EDC=90°-∠DFA,
∴△ADF∽△DCE,
∴$\frac{AD}{CD}=\frac{DF}{CE}$,
∴$\frac{4}{2}=\frac{x}{y}$,即y=$\frac{1}{2}$x.
∵点E在线段BC上,与点B、C不重合,
∴0<y<4,∴0<$\frac{1}{2}$x<4,即0<x<8,
∴y=$\frac{1}{2}$x,(0<x<8);
(2)①当点F线段DC上时,
∵CF=1,
∴DF=x=2-1=1,此时CE=y=$\frac{1}{2}$x=$\frac{1}{2}$;
②当点F线段DC延长线上时,
∵CF=1,
∴DF=x=2+1=3,此时CE=y=$\frac{1}{2}$x=$\frac{3}{2}$;
∴当CF=1时,EC的长为$\frac{1}{2}$或$\frac{3}{2}$.
点评 本题主要考查了矩形的性质、相似三角形的判定与性质、解方程等知识,对运算能力的要求比较高,当点的位置不确定、相似三角形的对应关系不确定时,常常需要分类讨论,避免出现漏解的现象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
 如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
 如图,在△ABC中,∠ACB=90°,CD⊥AB.垂足为D,E是AC的中点,ED、CB的延长线于点F.
如图,在△ABC中,∠ACB=90°,CD⊥AB.垂足为D,E是AC的中点,ED、CB的延长线于点F.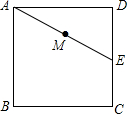 如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.
如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm. 如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点.
如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点. 如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.
如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.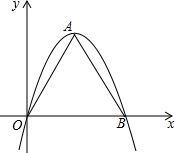 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.
如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.