题目内容
8.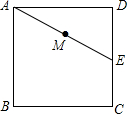 如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.
如图,已知正方形ABCD的边长是4cm,点E是CD的中点,连结AE,点M是AE的中点,过点M任意作直线分别与边AD、BC相交于点P、Q.若PQ=AE,则AP=$\frac{5}{2}$或$\frac{3}{2}$cm.
分析 如图,过点P作PH⊥BC交BC于H,先证明△PQH≌△AED推出∠AMP=90°,再利用△MAP∽△DAE,得$\frac{AP}{AE}$=$\frac{AM}{AD}$,求出AP,根据对称性求出AP′即可解决问题.
解答 解:如图,过点P作PH⊥BC交BC于H,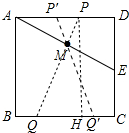
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠D=∠C=∠B=∠BAC=90°,
∵∠D=∠C=∠DPH=90°,
∴四边形PDCH是矩形,
∴PH=CD,
在△PQH和△AED中,
$\left\{\begin{array}{l}{PQ=AE}\\{PH=AD}\end{array}\right.$,
∴△PQH≌△AED,
∴∠DAE=∠QPH,
∵∠QPH+∠APM=90°,
∴∠DAE+∠APM=90°,
∴∠AMP=90°,
∵∠MAP=∠DAE,
∴△MAP∽△DAE,
∴$\frac{AP}{AE}$=$\frac{AM}{AD}$,
∵AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,AM=ME=$\sqrt{5}$,
∴$\frac{AP}{2\sqrt{5}}$=$\frac{\sqrt{5}}{4}$,
∴AP=$\frac{5}{2}$,PD=$\frac{3}{2}$,
根据对称性可得AP′=PD=$\frac{3}{2}$.
故答案为$\frac{5}{2}$或$\frac{3}{2}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,学会利用相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
17.已知点E(2,1)在二次函数y=x2-8x+m(m为常数)的图象上,则点E关于图象对称轴的对称点坐标是( )
| A. | (4,1) | B. | (5,1) | C. | (6,1) | D. | (7,1) |
20.若2x3-ax2-5x+5=(2x2+ax-1)(x-b)+3,其中a,b为整数,则a+b的值为( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
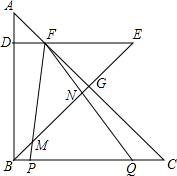 如图,△ABC是等腰直角三角形,点D在AB上,过D作DE⊥AB交AC于F,DE=BD,连接BE交AC于G.将一个45°角的顶点与点F重合,并绕点F旋转,这个角的两边分别交线段BC于P、Q两点,交BE于M、N两点.若AB=5,AD=1,CQ=1,则线段MN的长为$\frac{25\sqrt{2}}{14}$.
如图,△ABC是等腰直角三角形,点D在AB上,过D作DE⊥AB交AC于F,DE=BD,连接BE交AC于G.将一个45°角的顶点与点F重合,并绕点F旋转,这个角的两边分别交线段BC于P、Q两点,交BE于M、N两点.若AB=5,AD=1,CQ=1,则线段MN的长为$\frac{25\sqrt{2}}{14}$. 如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.
如图,在△ABC中,AB>AC,内切圆⊙I与边BC切于点D,AD与⊙I的另一个交点为E,⊙I的切线EP与BC的延长线交于点P,CF∥PE且与AD交于点F,直线BF与⊙I交于点M、N,M在线段BF上,线段PM与⊙I交于另一点Q.证明:∠ENP=∠ENQ.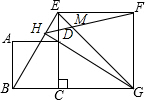 如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.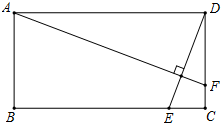 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.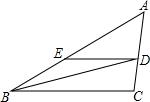 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.