题目内容
9.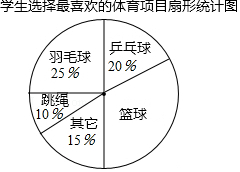 某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:学生选择最喜爱的体育项目统计表
| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 36 | 0.30 |
| 羽毛球 | m | 0.25 |
| 乒乓球 | 24 | n |
| 跳绳 | 12 | 0.10 |
| 其它项目 | 18 | 0.15 |
(1)统计表中的m=30,n=0.20;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为108度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.
分析 (1)根据篮球的人数和所占的百分比求出总人数,再用总人数乘以羽毛球所占的百分比,求出m的值;再用乒乓球的人数除以总人数,求出n的值;
(2)由于已知喜欢篮球的百分比,故可用360°乘以篮球所占的百分比,即可求出对应的扇形圆心角的度数;
(3)用总人数乘以最喜爱乒乓球的学生人数所占的百分比即可得出答案;
(4)根据题意先列出树状图,得出所有可能出现相同的结果数和两人都选择了最喜爱篮球的结果数,然后根据概率公式即可得出答案.
解答 解:(1)∵36÷0.3=120(人),
∴m=120×0.25=30(人),
n=24÷120=0.20,
故答案为:30,0.20;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为:360°×0.3=108°;
故答案为:108;
(3)根据题意得:
2400×0.2=480(人),
答:估计有480名学生最喜爱乒乓球;
(4)根据题意画树状图如下: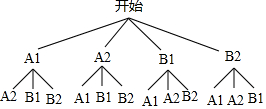
由表可知总共有12种结果,每种结果出现的可能性相同,其中两人都选择篮球的结果有2种,所以抽取的两人都选择了最喜爱篮球的概率是$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查了频率分布直方图,用到的知识点是频率=频数÷总数,概率公式,读懂统计表,运用数形结合思想来解决由统计图形式给出的数学实际问题是本题的关键.

练习册系列答案
相关题目
19.已知m,n分别是一个三角形的底和该底上的高,且满足(m-n)2=5,(m+n)2=11,则此三角形的面积为( )
| A. | 24 | B. | 12 | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
20.小刚从学校出发往东走1500m,再向南走1000m即可到家,选学校大门所在的位置为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表1m长,若以点A表示小刚家的位置,则点A的坐标是( )
| A. | (1500,-1000) | B. | (1500,1000) | C. | (-1000.1500) | D. | (-1500,1000) |
17.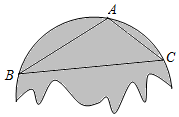 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )| A. | AB,AC边上的中线的交点 | B. | AB,AC边上的垂直平分线的交点 | ||
| C. | AB,AC边上的高所在直线的交点 | D. | ∠BAC与∠ABC的角平分线的交点 |
4.下列运算正确的是( )
| A. | (2a2)2=2a4 | B. | 6a8÷3a2=2a4 | C. | 2a2•a=2a3 | D. | 3a2-2a2=1 |
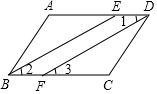 如图,在?ABCD中,BE,DF分别平分∠ABC,∠ADC.求证:BE∥DF.
如图,在?ABCD中,BE,DF分别平分∠ABC,∠ADC.求证:BE∥DF.