题目内容
20.小刚从学校出发往东走1500m,再向南走1000m即可到家,选学校大门所在的位置为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表1m长,若以点A表示小刚家的位置,则点A的坐标是( )| A. | (1500,-1000) | B. | (1500,1000) | C. | (-1000.1500) | D. | (-1500,1000) |
分析 由题意可知,小刚从学校出发往东走1500m,再向南走1000m即可到家,选学校大门所在的位置为原点建立坐标系,即可小刚家的坐标.
解答 解:学校大门所在的位置为原点,分别以正东、正北方向为x,y轴正方向建立平面直角坐标系,所以学校大门的坐标是(0,0),小刚家的坐标是(1500,-1000),
故选A.
点评 主要考查了直角坐标系的建立和运用,解决此类问题需要先确定原点的位置,再求未知点的位置.或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,在△ABC中,AB=CB,∠B=120°,AC=8,AB边的垂直平分线交AB于D,交AC于E,BC边的垂直平分线交BC于F,交AC于G,则EG的长是( )
如图,在△ABC中,AB=CB,∠B=120°,AC=8,AB边的垂直平分线交AB于D,交AC于E,BC边的垂直平分线交BC于F,交AC于G,则EG的长是( )
 如图,在△ABC中,AB=CB,∠B=120°,AC=8,AB边的垂直平分线交AB于D,交AC于E,BC边的垂直平分线交BC于F,交AC于G,则EG的长是( )
如图,在△ABC中,AB=CB,∠B=120°,AC=8,AB边的垂直平分线交AB于D,交AC于E,BC边的垂直平分线交BC于F,交AC于G,则EG的长是( )| A. | 8 | B. | $\frac{4}{3}$ | C. | 4 | D. | $\frac{8}{3}$ |
11.下列图示中,直线表示方法正确的有( )

| A. | ①②③④ | B. | ①② | C. | ②④ | D. | ①④ |
8. 如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为( )
如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为( )
 如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为( )
如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为( )| A. | 3:5 | B. | 4:5 | C. | 9:10 | D. | 15:16 |
15.若关于x的一元二次方程(k-1)x2+4x+1=0有实数根,则k的取值范围是( )
| A. | k≤5 | B. | k≤5,且k≠1 | C. | k<5,且k≠1 | D. | k<5 |
5.一组数据由五个正整数组成,中位数和众数都是2,则这五个数的和的最小值是( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
12.-8的绝对值是( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
9.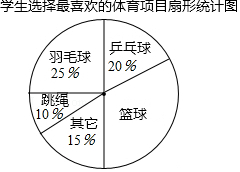 某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
学生选择最喜爱的体育项目统计表
请根据以上图表信息解答下列问题:
(1)统计表中的m=30,n=0.20;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为108度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.
 某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:学生选择最喜爱的体育项目统计表
| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 36 | 0.30 |
| 羽毛球 | m | 0.25 |
| 乒乓球 | 24 | n |
| 跳绳 | 12 | 0.10 |
| 其它项目 | 18 | 0.15 |
(1)统计表中的m=30,n=0.20;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为108度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.