题目内容
在平面直角坐标系中,梯形ABOC的顶点A(6,8)、C(10,0),AB∥OC,点P从C点出发,向点O运动(到达O点即停止运动),以PC为半径的⊙P与线段AC的另一个交点为D,与x轴的交点为F,过D作DE⊥OA于E.
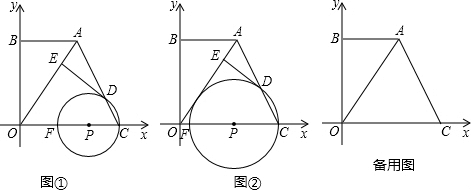
(1)求证:DE是⊙P的切线;
(2)当⊙P与OA相切时(如图②),求⊙P的半径;
(3)若以O为圆心,r为半径画⊙O,⊙O与⊙P相切.在运动过程中,当线段OA上有且只有一个点Q,使∠CQF=90°时,求此时r的大小或取值范围.

(1)求证:DE是⊙P的切线;
(2)当⊙P与OA相切时(如图②),求⊙P的半径;
(3)若以O为圆心,r为半径画⊙O,⊙O与⊙P相切.在运动过程中,当线段OA上有且只有一个点Q,使∠CQF=90°时,求此时r的大小或取值范围.
考点:圆的综合题
专题:
分析:(1)利用勾股定理得出AO的长,进而利用等腰三角形的性质以及平行线的判定定理得出∠OED=∠PDE=90°,即可得出答案;
(2)设⊙P与直线AO相切于点N,连接NP,利用相似三角形的判定与性质得出△AOB∽△OPN,则
=
,进而得出⊙P的半径;
(3)利用∠CQF=90°时.⊙P半径R=
或5<R<10,再利用当外切时,r+R=10-R,当内切时,R-r=10-R,5≤R<10,求出即可.
(2)设⊙P与直线AO相切于点N,连接NP,利用相似三角形的判定与性质得出△AOB∽△OPN,则
| OB |
| PN |
| AO |
| OP |
(3)利用∠CQF=90°时.⊙P半径R=
| 40 |
| 9 |
解答: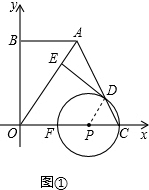 (1)证明:如图①,连接PD,
(1)证明:如图①,连接PD,
∵A(6,8)、C(10,0),
∴AB=6,BO=8,CO=10,
∴AO=CO=10,
∴∠OAC=∠OCA,
∵PD=PC,
∴∠PDC=∠PCD,
∴∠OAC=∠PDC,
∴AO∥PD,
∴∠OED=∠PDE=90°,
∴DE是⊙P的切线;
(2)解:如图②,

设⊙P与直线AO相切于点N,连接NP,
由题意可得出:PN⊥AO,
∵∠BOA+∠AOC=90°,∠AOP+∠OPN=90°,
∴∠BOA=∠OPN,
又∵∠ABO=∠ONP=90°,
∴△AOB∽△OPN,
∴
=
,
设NP=x,则OP=10-x,
故
=
,
解得:x=
,
即⊙P的半径为:
;
(3)解:∵线段OA上有且只有一个点Q,使∠CQF=90°时,
∴⊙P与线段OA只有一个共公点,
∴⊙P半径R=
或5<R<10,
当外切时,r+R=10-R,
解得:r=
当内切时,R-r=10-R,5≤R<10,
故0≤r<10
综上:此时r的大小或取值范围是:0≤r<10.
 (1)证明:如图①,连接PD,
(1)证明:如图①,连接PD,∵A(6,8)、C(10,0),
∴AB=6,BO=8,CO=10,
∴AO=CO=10,
∴∠OAC=∠OCA,
∵PD=PC,
∴∠PDC=∠PCD,
∴∠OAC=∠PDC,
∴AO∥PD,
∴∠OED=∠PDE=90°,
∴DE是⊙P的切线;
(2)解:如图②,

设⊙P与直线AO相切于点N,连接NP,
由题意可得出:PN⊥AO,
∵∠BOA+∠AOC=90°,∠AOP+∠OPN=90°,
∴∠BOA=∠OPN,
又∵∠ABO=∠ONP=90°,
∴△AOB∽△OPN,
∴
| OB |
| PN |
| AO |
| OP |
设NP=x,则OP=10-x,
故
| 8 |
| x |
| 10 |
| 10-x |
解得:x=
| 40 |
| 9 |
即⊙P的半径为:
| 40 |
| 9 |
(3)解:∵线段OA上有且只有一个点Q,使∠CQF=90°时,
∴⊙P与线段OA只有一个共公点,
∴⊙P半径R=
| 40 |
| 9 |
当外切时,r+R=10-R,
解得:r=
| 10 |
| 9 |
当内切时,R-r=10-R,5≤R<10,
故0≤r<10
综上:此时r的大小或取值范围是:0≤r<10.
点评:此题主要考查了圆的综合应用以及相似三角形的判定与性质和切线的判定等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
 如图:
如图:
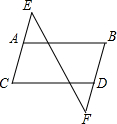 如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.
如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.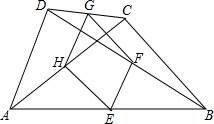 如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.