题目内容
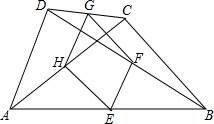 如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是
考点:中点四边形
专题:
分析:(1)证得EF∥GH,EF=GH后利用一组对边平行且相等的四边形是平行四边形判定即可;
(2)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AD且EF=
AD,同理可得GH∥AD且GH=
AD,EH∥BC且EH=
BC,然后证明四边形EFGH是平行四边形,再根据邻边相等的平行四边形是菱形解答.
(2)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AD且EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)四边形EFGH是平行四边形;
证明:在△ACD中∵G、H分别是CD、AC的中点,
∴GH∥AD,GH=
AD,
在△ABC中∵E、F分别是AB、BD的中点,
∴EF∥AD,EF=
AD,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形.
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AD=BC.
理由如下:∵E,F分别是AB,BD的中点,
∴EF∥AD且EF=
AD,
同理可得:GH∥AD且GH=
AD,EH∥BC且EH=
BC,
∴EF∥GH且EF=GH,
∴四边形EFGH是平行四边形,
∵AD=BC,
∴
AD=
BC,
即EF=EH,
∴?EFGH是菱形.
证明:在△ACD中∵G、H分别是CD、AC的中点,
∴GH∥AD,GH=
| 1 |
| 2 |
在△ABC中∵E、F分别是AB、BD的中点,
∴EF∥AD,EF=
| 1 |
| 2 |
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形.
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AD=BC.
理由如下:∵E,F分别是AB,BD的中点,
∴EF∥AD且EF=
| 1 |
| 2 |
同理可得:GH∥AD且GH=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF∥GH且EF=GH,
∴四边形EFGH是平行四边形,
∵AD=BC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
即EF=EH,
∴?EFGH是菱形.
点评:本题考查了菱形的判定,平行四边形的判定,三角形的中位线定理,根据三角形的中位线平行于第三边并且等于第三边的一半得到四边形EFGH的对边平行且相等从而判定出平行四边形是解题的关键,也是本题的突破口.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
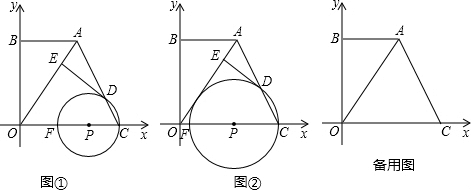
 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为
如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为