题目内容

已知a是方程x2+5x=14的根，求（2a-11）（a-1）-（a+1）2+（3+2a）（3-2a）的值．
考点：整式的混合运算—化简求值,解一元二次方程-因式分解法
专题：
分析：求出a2+5a=1，先算乘法，再合并同类项，变形后代入求出即可．
解答：解：∵a是方程x2+5x=14的根，
∴a2+5a=1，
∴（2a-11）（a-1）-（a+1）2+（3+2a）（3-2a）
=2a2-2a-11a+11-a2-2a-1+9-4a2
=-3a2-15a+19
=-3（a2+5a）+19
=-3×1+19
=16．
点评：本题考查了求代数式的值，一元二次方程的解的定义的应用，用了整体代入思想，题目比较好，难度适中．
练习册系列答案
相关题目
解不等式：
x+4
6
-
x
3
≤x-4．
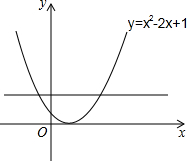如果抛物线m的顶点在抛物线n上，同时抛物线n的顶点在抛物线m上，那么我们就称抛物线m与n为交融抛物线．
（1）已知抛物线a：y=x2-2x+1．判断下列抛物线b：y=x2-2x+2，c：y=-x2+4x-3与已知抛物线a是否为交融抛物线？并说明理由；
（2）在直线y=2上有一动点P（t，2），将抛物线a：y=x2-2x+1绕点P（t，2）旋转180°得到抛物线l，若抛物线a与l为交融抛物线，求抛物线l的解析式；
（3）M为抛物线a；y=x2-2x+1的顶点，Q为抛物线a的交融抛物线的顶点，是否存在以MQ为斜边的等腰直角三角形MQS，使其直角顶点S在y轴上？若存在，求出点S的坐标；若不存在，请说明理由；
（4）通过以上问题的探究解决，相信你对交融抛物线的概念及性质有了一定的认识，请你提出一个有关交融抛物线的问题．
已知：关于x的方程mx2+（3m+1）x+3=0．
（1）求证：不论m为任何实数，此方程总有实数根；
（2）如果该方程有两个不同的整数根，且m为正整数，求m的值；
（3）在（2）的条件下，令y=mx2+（3m+1）x+3，如果当x1=a与x2=a+n（n≠0）时有y1=y2，求代数式4a2+12an+5n2+16n+8的值．
把下列各式分解因式：
（1）mn2+6mn+9m；              
（2）4x2（a-b）+（b-a）．
在平面直角坐标系中，梯形ABOC的顶点A（6，8）、C（10，0），AB∥OC，点P从C点出发，向点O运动（到达O点即停止运动），以PC为半径的⊙P与线段AC的另一个交点为D，与x轴的交点为F，过D作DE⊥OA于E．

（1）求证：DE是⊙P的切线；
（2）当⊙P与OA相切时（如图②），求⊙P的半径；
（3）若以O为圆心，r为半径画⊙O，⊙O与⊙P相切．在运动过程中，当线段OA上有且只有一个点Q，使∠CQF=90°时，求此时r的大小或取值范围．
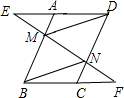已知，如图，在平行四边形ABCD中，点M，N分别在边AB，DC上，作直线MN，分别交DA和BC的延长线于点E，F，且AE=CF．
（1）求证：△AEM≌△CFN；
（2）求证：四边形BNDM是平行四边形．
化简：（
1
a+1
+
a-1
a2-1
）÷
2
a+1
．
若4a2+2ka+9是一个完全平方式，则k等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网