题目内容
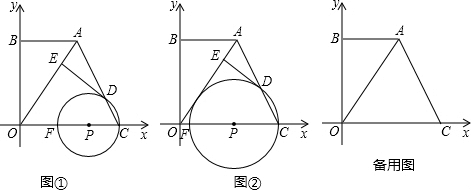
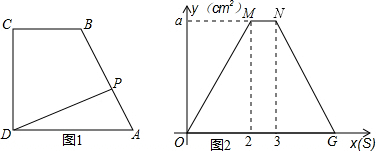
如图1,在直角梯形ABCD中,BC∥AD,CD⊥AD,∠A=60°.动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,当点P到达点D时停止运动.已知△PAD的面积y(cm2)与点P的运动时间x(s)的函数关系如图2,请你根据图象提供的信息,解答下列问题:
(1)AB= cm,BC= cm.
(2)①求a的值与点G的坐标;②用文字说明点N坐标所表示的实际意义.
(1)AB=
(2)①求a的值与点G的坐标;②用文字说明点N坐标所表示的实际意义.

考点:动点问题的函数图象
专题:
分析:(1)利用P点运动的速度以及结合函数图象得出AB以及BC的长;
(2)①当点P运动到点B时,△PAD的面积为a;作BH⊥AD,垂足为H,进而求出BH的长,进而得出S△BAD,进而得a的值,求出G点坐标即可;
②利用a的值得出N点坐标,进而得出答案.
(2)①当点P运动到点B时,△PAD的面积为a;作BH⊥AD,垂足为H,进而求出BH的长,进而得出S△BAD,进而得a的值,求出G点坐标即可;
②利用a的值得出N点坐标,进而得出答案.
解答: 解:(1)∵动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,
解:(1)∵动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,
∴由图象可得出P点在AB上运动了2秒,故运动的路程为:2×2=4(cm),
∵动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,
∴由图象可得出P点在AB上运动了1秒,故运动的路程为:1×2=2(cm),
故答案为:4,2.
(2)①由函数图象可知,AB=2×2=4cm,BC=1×2=2cm.
当点P运动到点B时,△PAD的面积为a;作BH⊥AD,垂足为H.
在Rt△BHA中,由∠A=60°,AB=4,得BH=AB×sin60°=2
,
∴S△BAD=
×4×2
=4
,即a=4
.
∵P从点A出发沿AB-BC-CD运动到达点D时路程为:
(4+2+2
)=6+2
(cm),
∴运动时间为(6+2
)÷2=3+
(s),
即点G的坐标为(3+
,0).
②点N的坐标为(3,4
),它表示的实际意义为:当点P从A出发沿AB-BC运动3s时到达点C,此时△PAD的面积为4
cm2.
 解:(1)∵动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,
解:(1)∵动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,∴由图象可得出P点在AB上运动了2秒,故运动的路程为:2×2=4(cm),
∵动点P从点A出发,以2cm∕s的速度沿折线AB-BC-CD运动,
∴由图象可得出P点在AB上运动了1秒,故运动的路程为:1×2=2(cm),
故答案为:4,2.
(2)①由函数图象可知,AB=2×2=4cm,BC=1×2=2cm.
当点P运动到点B时,△PAD的面积为a;作BH⊥AD,垂足为H.
在Rt△BHA中,由∠A=60°,AB=4,得BH=AB×sin60°=2
| 3 |
∴S△BAD=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
∵P从点A出发沿AB-BC-CD运动到达点D时路程为:
(4+2+2
| 3 |
| 3 |
∴运动时间为(6+2
| 3 |
| 3 |
即点G的坐标为(3+
| 3 |
②点N的坐标为(3,4
| 3 |
| 3 |
点评:此题主要考查了动点函数图象的应用,利用数形结合得出AB,BC的长是解题关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
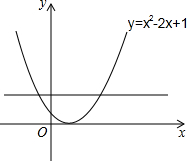 如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.
如果抛物线m的顶点在抛物线n上,同时抛物线n的顶点在抛物线m上,那么我们就称抛物线m与n为交融抛物线.