题目内容
20.如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.(1)求抛物线的解析式;
(2)说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
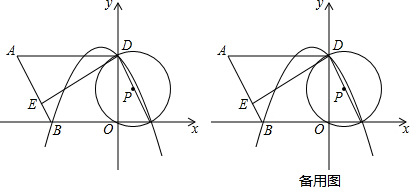
分析 (1)解直角三角形得到D(0,2$\sqrt{3}$),设抛物线的解析式为y=(x+4)(x-2),把D(0,2$\sqrt{3}$)即可得到结论;
(2)根据平行四边形的性质得到AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,根据相似三角形的性质得到∠ADE=∠CDO,于是得到CD为⊙P的直径,根据切线的判定定理得到ED是⊙P的切线;E点的对应点E′不会落在抛物线上,根据相似三角形的想知道的DE=3$\sqrt{3}$,根据旋转的想知道的E点的对应点在射线DC上,而点D,C在抛物线上,于是得到点E′不能在抛物线上;
(3)根据二次函数的解析式得到M(-1,$\frac{9\sqrt{3}}{4}$),由B(-4,0),D(0,2$\sqrt{3}$),当BM为平行四边形BDMN的对角线时,当DM为平行四边形BDMN的对角线时,当BD为平行四边形BDMN的对角线时,根据平移的性质即可得到结论.
解答  解:(1)∵C点坐标为(2,0),BC=6,
解:(1)∵C点坐标为(2,0),BC=6,
∴B(-4,0),
在Rt△OCD中,∵tan∠OCD=$\frac{OD}{OC}$,
∴OD=2tan60°=2$\sqrt{3}$,
∴D(0,2$\sqrt{3}$),
设抛物线的解析式为y=(x+4)(x-2),
把D(0,2$\sqrt{3}$)代入得a•4•(-2)=2$\sqrt{3}$,
解得:a=-$\frac{\sqrt{3}}{4}$,
∴抛物线的解析式为y=-$\frac{\sqrt{3}}{4}$(x+4)(x-2)=-$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$;
(2)在Rt△OCD中,CD=2OC=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,
∵AE=3BE,
∴AE=3,
∴$\frac{AE}{OC}=\frac{3}{2}$,$\frac{AD}{CD}$=$\frac{6}{4}$=$\frac{3}{2}$,
∴$\frac{AE}{OC}=\frac{AD}{CD}$,
∵∠DAE=∠DCB,
∴△AED∽△DCB,
∴∠ADE=∠CDO,
∵∠ADE+∠ODE=90°,
∴∠CDO+∠ODE=90°,
∴CD⊥DE,
∵∠DOC=90°,
∴CD为⊙P的直径,
∴ED是⊙P的切线;
E点的对应点E′不会落在抛物线上,
理由:∵△AED∽△COD,
∴$\frac{DE}{OD}=\frac{AE}{OC}$,
即$\frac{DE}{2\sqrt{3}}$=$\frac{3}{2}$,
解得:DE=3$\sqrt{3}$,
∵∠CDE=90°,DE>DC,
∴将△ADE绕点D逆时针旋转90°,E点的对应点在射线DC上,而点D,C在抛物线上,
∴点E′不能在抛物线上;
(3)存在,∵y=-$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x+2$\sqrt{3}$=-$\frac{\sqrt{3}}{4}$(x+1)2+$\frac{9\sqrt{3}}{4}$,
∴M(-1,$\frac{9\sqrt{3}}{4}$),
∵B(-4,0),D(0,2$\sqrt{3}$),
如图,当BM为平行四边形BDMN的对角线时,
点D向左平移4个单位,再向下平移2$\sqrt{3}$个单位得到B,
则点M(-1,$\frac{9\sqrt{3}}{4}$)向左平移4个单位,再向下平移2$\sqrt{3}$个单位得到N1(-5,$\frac{\sqrt{3}}{4}$);
当DM为平行四边形BDMN的对角线时,
点B向右平移3个单位,再向上平移$\frac{9\sqrt{3}}{4}$个单位得到D,
则点M(-1,$\frac{9\sqrt{3}}{4}$)向右平移4个单位,再向上平移2$\sqrt{3}$个单位得到N2(3,$\frac{17\sqrt{3}}{4}$);
当BD为平行四边形BDMN的对角线时,
点M向右平移1个单位,再向下平移$\frac{\sqrt{3}}{4}$个单位得到D,
则点B(-4,0)向右平移1个单位,再向下平移$\frac{\sqrt{3}}{4}$个单位得到N3(-3,-$\frac{\sqrt{3}}{4}$);
综上所述,以点B,D,M,N为顶点的四边形为平行四边形时,点N的坐标为(-5,$\frac{\sqrt{3}}{4}$)或(3,$\frac{17\sqrt{3}}{4}$)或(-3,-$\frac{\sqrt{3}}{4}$).
点评 本题考查了求抛物线的解析式,解直角三角形,旋转的性质,相似三角形的判定和性质,平行四边形的判定和性质,切线的判定,正确的作出图形是解题的关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案| A. | 相反数 | B. | 绝对值 | C. | 平方数 | D. | 倒数 |
| A. | -$\frac{2}{3}$ | B. | -1 | C. | -|-$\sqrt{3}$| | D. | 3-2 |
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的6倍 | D. | 是原来的9倍 |
| A. | 9 | B. | 8 | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
| A. | 图象经过第一、二、三象限 | B. | 图象经过点(-2,1) | ||
| C. | 当x>1时,y<0 | D. | y随x的增大而增大 |
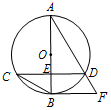 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.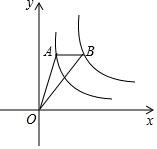 如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )
如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )